分类： 赛事资讯

2010年 AIME II 数学邀请赛真题和答案解析

2010年 AIME II 数学邀请赛真题

问题 1

设为所有数字都是偶数且没有两个数字相同的数$N$的最大整数倍。求除以时的余数。 $36$$N$$1000$

问题 2

$P$在单位正方形 内部随机选取一点$S$。设表示从到 的最近边的$d(P)$距离。等于 的概率，其中和为互质正整数。求。 $P$$S$$\frac{1}{5}\le d(P)\le\frac{1}{3}$$\frac{m}{n}$$百万$$n$$m+n$

问题 3

设是所有因数（不一定不同）$K$的乘积，其中和是满足的整数。找出能够整除的最大正整数。 $(ba)$$a$$b$$1\le a < b \le 20$$n$$2^n$$K$

问题4

戴夫到达一个机场，该机场有 12 个登机口，排列成一条直线，$100$相邻登机口之间的距离恰好为英尺。他的登机口是随机分配的。在登机口等待后，戴夫被告知登机口已更改为另一个登机口，同样是随机的。假设戴夫步行$400$几英尺或更短时间到达新登机口的概率为分数$\frac{m}{n}$，其中$百万$和$n$是互质正整数。求$m+n$。

问题5

正数$x$、$y$、 和$z$满足$xyz = 10^{81}$和$(\log_{10}x)(\log_{10} yz) + (\log_{10}y) (\log_{10}z) = 468$。求$\sqrt {(\log_{10}x)^2 + (\log_{10}y)^2 + (\log_{10}z)^2}$。

问题 6

寻找最小的正整数$n$，其特性是多项式$x^4 - nx + 63$可以写成两个具有整数系数的非常数多项式的乘积。

问题 7

设$P(z)=z^3+az^2+bz+c$，其中$a$，$b$和$c$为实数。存在一个复数，$w$使得 的三个根分别$P(z)$为$w+3i$，$w+9i$和$2周到4美元，其中$i^2=-1$。求$|a+b+c|$。

问题 8

设$N$是非空集的有序对的数量$\mathcal{A}$，并$\mathcal{B}$具有以下属性：

  • $\mathcal{A} \cup \mathcal{B} = \{1,2,3,4,5,6,7,8,9,10,11,12\}$，
  • $\mathcal{A} \cap \mathcal{B} = \emptyset$，
  • 元素的数量$\mathcal{A}$不是 的元素$\mathcal{A}$，
  • 元素的数量$\mathcal{B}$不是 的元素$\mathcal{B}$。

寻找$N$。

问题 9

设$ABCDEF$为正六边形。设黄金、$H$、$我$、$J$、$K$和分别为边、、、、和$L$的中点。线段、、、、 和构成一个较小的正六边形。设小六边形的面积与 的面积之比用分数表示，其中和是互质正整数。求。 $AB$BC$CD$德意志银行$EF$$AF$$\overline{AH}$$\overline{BI}$$\overline{CJ}$$\overline{DK}$$\overline{EL}$$\overline{FG}$$ABCDEF$$\frac {m}{n}$$百万$$n$$m + n$

问题 10

求出具有整数系数和整数零点的二次多项式的数量$f(x)$，使得$f(0)=2010$。

问题11

将T 网格定义为$3\times3$满足以下两个属性的矩阵：

  1. 其中恰好有五个条目是$1$，其余四个条目是$0$。
  2. 在八行、八列、八条长对角线（长对角线为$\{a_{13},a_{22},a_{31}\}$和$\{a_{11},a_{22},a_{33}\})$）中，最多只有一条线的三个元素相等。

找出不同T 型网格的数量。

问题 12

两个不全等的整数边等腰三角形周长和面积相等。两个三角形底边的长度比为$8: 7美元。求出它们公共周长的最小可能值。

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2010年 AIME I 数学邀请赛真题和答案解析

2010年 AIME I 数学邀请赛真题

问题 1

Maya 列出了 的所有正因数$2010^2$。然后她从这个列表中随机选择两个不同的因数。设$p$为所选因数中恰好有一个是完全平方数的概率。该概率$p$可以表示为 的形式$\frac {m}{n}$，其中$百万$和$n$是互质正整数。求$m + n$。

问题 2

$9 \times 99 \times 999 \times \cdots \times \underbrace{99\cdots9}_{\text{999 个 9}}$求除以 的余数$1000$。

问题 3

假设$y = \frac34x$和$x^y = y^x$。数量$x + y$可以表示为有理数$\frac {r}{s}$，其中$r$和$s$是互质正整数。求$r + s$。

问题4

Jackie 和 Phil 有两枚公平硬币和一枚第三枚硬币，硬币正面朝上的概率为$\frac47$。Jackie 抛三枚硬币，然后 Phil 也抛三枚硬币。设$\frac {m}{n}$为 Jackie 抛出正面的次数与 Phil 抛出次数相同的概率，其中$百万$和$n$为互质正整数。求$m + n$。

问题5

正整数$a$、$b$、$c$和$d$满足$a>b>c>d$、$a + b + c + d = 2010$、 和$a^2-b^2+c^2-d^2=2010$。求 的可能值的数量$a$。

问题 6

设$P(x)$是具有实系数的二次多项式，且$x^2 - 2x + 2 \le P(x) \le 2x^2 - 4x + 3$对所有实数都满足$x$，并假设$P(11) = 181$。求$P(16)$。

问题 7

定义一个有序集合三元$(A, B, C)$组为$\textit{最小相交}$若$|A \cap B| = |B \cap C| = |C \cap A| = 1$且为$A \cap B \cap C = \emptyset$。例如，$（\{1,2\},\{2,3\},\{1,3,4\}）$是一个最小相交三元组。设$N$是最小相交有序集合三元组的数量，其中每个集合都是 的子集。当除以$\{1,2,3,4,5,6,7\}$时，求余数。 $N$$1000$

注：$|S|$表示集合中元素的数量$S$。

问题 8

对于实数$a$，设$\lfloor a \rfloor$表示小于或等于 的最大整数$a$。设$\mathcal{R}$表示坐标平面中由$(x,y)$这样的点组成的区域$\lfloor x \rfloor ^2 + \lfloor y \rfloor ^2 = 25$。该区域$\mathcal{R}$完全包含在半径为 的圆盘中$r$（圆盘是圆及其内部的并集）。 的最小值$r$可以写成$\frac {\sqrt {m}}{n}$，其中$百万$和$n$是整数，$百万$不能被任何素数的平方整除。求$m + n$。

问题 9

设$(a,b,c)$是方程组$x^3-xyz=2$、$y^3 - xyz = 6$、的实数解$z^3-xyz=20$。 的最大可能值$a^3 + b^3 + c^3$可以写成 的形式$\frac {m}{n}$，其中$百万$和$n$是互质正整数。求$m + n$。

问题 10

设为写成形式$N$的方法数，其中为整数，且。这种表示的一个例子是。求。 $2010$$2010 = a_3 \cdot 10^3 + a_2 \cdot 10^2 + a_1 \cdot 10 + a_0$$a_i$$0 \le a_i \le 99$$1\cdot 10^3 + 3\cdot 10^2 + 67\cdot 10^1 + 40\cdot 10^0$$N$

问题11

设是坐标平面中满足和的$\mathcal{R}$点集所构成的区域。当绕直线旋转时，其方程为，则所得立体的体积为，其中，，和为正整数，和互质，不能被任何质数的平方整除。求。 $|8 - x| + y ≤ 10$$3y - x \ge 15$$\mathcal{R}$$3y - x = 15$$\frac {m\pi}{n\sqrt {p}}$$百万$$n$$p$$百万$$n$$p$$m + n + p$

问题 12

设$m \ge 3$为整数，且$S = \{3,4,5,\ldots,m\}$。求 的最小值，使得$百万$对于 的每个$S$两个子集的划分，至少有一个子集包含整数$a$、$b$和$c$（不一定不同），使得$ab = c$。

注意： 的划分$S$是一对集合$A$，$B$使得$A \cap B = \emptyset$。$A \cup B = S$

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2011年 AIME II 数学邀请赛真题和答案解析

2011年 AIME II 数学邀请赛真题

问题 1

加里买了一大杯饮料，但只喝了一半$m/n$，其中$百万$和$n$是互质正整数。如果他买的量是原来的一半，喝的量是原来的两倍，那么他浪费的$2/9$饮料就只有原来的一半。求$m+n$。

问题 2

在正方形上$ABCD$，点$E$位于边上$AD$，点$F$位于边上BC$，使得$BE=EF=FD=30$。求正方形的面积$ABCD$。

问题 3

凸 18 边形中各个角度的度数构成一个具有整数值的递增等差数列。求出最小角度的度数。

问题4

在三角形中$ABC$，$AB=20$和$AC=11$。角的角平分线$A$交BC$于点$D$，点$M$是 的中点$AD$。设为和直线$P$的交点。到的比值可以表示为 的形式，其中和是互质正整数。求。 $AC$$BM$CP$帕拉梅拉$\frac{m}{n}$$百万$$n$$m+n$

问题5

$2011$等比数列的首项之和为$200$。首$4022$项之和为$380$。求首$6033$项之和。

问题 6

如果，且，则将有序整数四元组定义$（a，b，c，d）$为有趣的。有多少个有趣的有序四元组？ $1 \le a<b<c<d \le 10$$a+d>b+c$

问题 7

埃德有五颗相同的绿色弹珠和大量相同的红色弹珠。他将绿色弹珠和一些红色弹珠排成一排，发现其右手边相邻的弹珠颜色与自己相同，其右手边相邻的弹珠颜色不同。这种排列的一个例子是 GGRRRGGRG。设 为$百万$可以进行这种排列的最大红色弹珠数量，设 为$N$他可以满足$m+5$要求的排列弹珠的方式数量。求当$N$除以时的余数$1000$。

问题 8

设$z_1,z_2,z_3,\dots,z_{12}$为多项式 的12个零点$z^{12}-2^{36}$。对于每个$j$，设为或$w_j$之一。则 的实部的最大可能值可以写成其中和为正整数。求。 $z_j$$i z_j$$\sum_{j=1}^{12} w_j$$m+\sqrt{n}$$百万$$n$$m+n$

问题 9

设$ x_1 $，$ x_2 $，$\dots$，$x_6$为非负实数$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 1$，且$x_1x_3x_5 + x_2x_4x_6 \ge {\frac{1}{540}}$， 。设$p$和$q$为互质正整数，且$\frac{p}{q}$为 的最大可能值$x_1x_2x_3 + x_2x_3x_4 + x_3x_4x_5 + x_4x_5x_6 + x_5x_6x_1 + x_6x_1x_2$。求$p + q$。

问题 10

一个圆心为25 的圆，长度为 30 的$O$弦与长度为 14 的弦相交于点，两弦中点之间的距离为 12 ，该量可以表示为，其中和为互质正整数，求除以 1000 时的余数。 $\overline{AB}$$\overline{CD}$$P$$OP^2$$\frac{m}{n}$$百万$$n$$m + n$

问题11

设$M_n$为矩阵$n \乘以 n$，其元素如下：对于$1 \le i \le n$，$m_{i,i} = 10$；对于$1 \le i \le n - 1$，$m_{i+1,i} = m_{i,i+1} = 3$；中的所有其他元素$M_n$均为零。设$D_n$为矩阵 的行列式$M_n$。则可$\sum_{n=1}^{\infty} \frac{1}{8D_n+1}$表示为$\frac{p}{q}$，其中$p$和$q$为互质正整数。求$p + q$。

$1 \乘以 1$注意：矩阵的行列式$[a]$为，矩阵$a$的行列式；对于，首行或首列为 的矩阵，其行列式等于，其中是去掉包含 的行和列后得到的矩阵的行列式。 $2 \乘以 2$$\left[ {\begin{array}{cc} a & b \\ c & d \\ \end{array} } \right] = ad - bc$$n \ge 2$$n \乘以 n$$a_1$ $a_2$ $a_3$ $\dots$ $a_n$$a_1C_1 - a_2C_2 + a_3C_3 - \dots + (-1)^{n+1}a_nC_n$$C_i$$(n - 1) \times (n - 1)$$a_i$

问题 12

九位代表，每人来自三个不同的国家，随机选择一张可容纳九人的圆桌旁的椅子。假设每位代表坐在至少一个来自其他国家的代表旁边的概率为$\frac{m}{n}$，其中$百万$和$n$是互质正整数。求$m + n$。

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2011年 AIME I 数学邀请赛真题和答案解析

2011年 AIME I 数学邀请赛真题

问题 1

罐子里$A$装有四升酸性溶液$45\%$。罐子里$B$装有五升酸性溶液$48\%$。罐子里加元装有一升酸性溶液$k\%$。从罐子中加元，$\frac{m}{n}$将几升溶液加入到罐子中$A$，将罐子中剩余的溶液加元加入到罐子 B 中。最后，罐子$A$和罐子中都$B$装有$50\%$酸性溶液。假设$百万$和$n$是互质正整数，求$k + m + n$。

问题 2

在矩形 中$ABCD$，$AB = 12$和BC=10美元。点$E$和$F$位于矩形内，$ABCD$使得$BE = 9$、$DF = 8$、$\overline{BE} \parallel \overline{DF}$、$\overline{EF} \parallel \overline{AB}$，且线段$BE$相交$\overline{AD}$。长度$EF$可以表示为 的形式$m \sqrt{n} - p$，其中$百万$、$n$、 和$p$为正整数，且不$n$能被任何素数的平方整除。求$m + n + p$。

问题 3

设为包含点 的$L$斜率直线，设为包含点 的垂直于直线的直线。删除原坐标轴，将直线设为轴，直线 设为轴。在新坐标系中，点在正轴上，点在正轴上。原坐标系中坐标为 的点在新坐标系中坐标为。求。 $\frac{5}{12}$$A = (24,-1)$$M$$L$$B = (5,6)$$L$$x$$M$$y$$A$$x$$B$$y$$P$$(-14,27)$$（\alpha，\beta）$$\alpha + \beta$

问题4

在三角形中$ABC$，$AB = 125$，$AC = 117$和BC 美元 = 120 美元。 角的角$A$平分线交$\overline{BC}$于点$L$， 角的角平分线$B$交$\overline{AC}$于点$K$。设$M$和分别为从到和 的$N$垂线的脚。求。 加元$\overline{BK}$$\overline{AL}$百万

问题5

一个正九边形（9 边形）的顶点应标有数字 1 到 9，并且每三个连续顶点上的数字之和是 3 的倍数。如果可以通过在平面中旋转九边形获得一种可接受的排列，则认为两种可接受的排列无法区分。求出可区分的可接受排列的数量。

问题 6

假设抛物线有顶点$\left(\frac{1}{4},-\frac{9}{8}\right)$和方程$y = ax^2 + bx + c$，其中$a > 0$和$a + b + c$为整数。的最小可能值$a$可以写成形式$\frac{p}{q}$，其中$p$和$q$为互质正整数。求$p + q$。

问题 7

$百万$求出存在非负整数$x_0$, $ x_1 $,的正整数个数$\dots$，$x_{2011}$满足\[m^{x_0} = \sum_{k = 1}^{2011} m^{x_k}.\]

问题 8

在三角形中$ABC$，BC 元 = 23 美元，加元 = 27美元和$AB = 30$。点$V$和$W$在 上，在$\overline{AC}$上$V$，$\overline{AW}$点$X$和$Y$在 上$\overline{BC}$，$X$在 上$\overline{CY}$，点$Z$和$U$在 上，$\overline{AB}$在$Z$上$\overline{BU}$。此外，点的位置使得$\overline{UV} \parallel \overline{BC}$，$\overline{WX} \parallel \overline{AB}$和。然后沿，和$\overline{YZ} \parallel \overline{CA}$进行直角折叠。将得到的图形放在水平地板上，做成一个带有三角形腿的桌子。设是由顶部与地板平行的三角形构成的桌子的最大可能高度。然后可以写成 的形式，其中和是互质正整数，是不能被任何素数的平方整除的正整数。求。 $\overline{UV}$$\overline{WX}$$\overline{YZ}$$h$$ABC$$h$$\frac{k \sqrt{m}}{n}$$k$$n$$百万$$k + m + n$

[asy] unitize(1 cm); 成对翻译; 对[] A，B，C，U，V，W，X，Y，Z; A[0] = (1.5,2.8); B[0] = (3.2,0); C[0] = (0,0); U[0] = (0.69*A[0] + 0.31*B[0]); V[0] = (0.69*A[0] + 0.31*C[0]); W[0] = (0.69*C[0] + 0.31*A[0]); X[0] = (0.69*C[0] + 0.31*B[0]); Y[0] = (0.69*B[0] + 0.31*C[0]); Z[0] = (0.69*B[0] + 0.31*A[0]); 翻译 = (7,0); A[1] = (1.3,1.1) + 平移; B[1] = (2.4,-0.7) + 平移; C[1] = (0.6,-0.7) + 平移; U[1] = U[0] + 平移; V[1] = V[0] + 平移; W[1] = W[0] + 平移; X[1] = X[0] + 平移; Y[1] = Y[0] + 平移; Z[1] = Z[0] + 平移; 绘制（A[0]--B[0]--C[0]--循环）；绘制（U[0]--V[0]，虚线）；绘制（W[0]--X[0]，虚线）；绘制（Y[0]--Z[0]，虚线）；绘制（U[1]--V[1]--W[1]--X[1]--Y[1]--Z[1]--循环）；绘制（U[1]--A[1]--V[1]，虚线）；绘制（W[1]--C[1]--X[1]）；绘制（Y[1]--B[1]--Z[1]）；点（“$A$”，A[0]，N）；点（“$B$”，B[0]，SE）；点（“$C$”，C[0]，SW）；点（“$U$”，U[0]，NE）；点（“$V$”，V[0]，NW）；点（“$W$”，W[0]，NW）；点（“$X$”，X[0]，S）；点（“$Y$”，Y[0]，S）；点（“$Z$”，Z[0]，NE）；点（A[1]）；点（B[1]）；点（C[1]）；点（“$U$”，U[1]，NE）；点("$V$",V[1],NW);点("$W$",W[1],NW);点("$X$",X[1],dir(-70));点("$Y$",Y[1],dir(250));点("$Z$",Z[1],NE);[/asy]

问题 9

设$x$在区间$[0,\pi/2]$和内$\log_{24 \sin x} (24 \cos x) = \frac{3}{2}$。求$24 \cot^2 x$。

问题 10

从正边形的顶点中随机选取三个不同顶点的集合$n$构成钝角三角形的概率为$\frac{93}{125}$。求出 的所有可能值的和$n$。

问题11

设为非负整数 形式数除以 1000 时$R$所有可能余数的集合。设为 中元素之和。求除以 1000 时的余数。$2^n$$n$$S$$R$$S$

问题 12

六名男子和一定数量的妇女以随机顺序站成一排。假设$p$每名男子旁边至少站着一名男子，则设至少有四名男子站在一起的概率为。找出队伍中女性人数最少的人数，使之$p$不超过 1%。

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2012年 AIME II 数学邀请赛真题和答案解析

2012年 AIME II 数学邀请赛真题

问题 1

$（m，n）$求出方程的正整数解的有序对的数量2000 万美元 + 12n = 2012 美元。

问题 2

两个等比数列$a_1, a_2, a_3, \ldots$和$b_1, b_2, b_3, \ldots$有相同的公比，即$a_1 = 27$，，$b_1=99$和$a_{15}=b_{11}$。求$a_9$。

问题 3

某大学数学系下设数学系、统计学系和计算机科学系，每个系有两名男教授和两名女教授，一个由六名教授组成的委员会应包含三名男教授和三名女教授，并且还必须包含来自三个系的两名教授。求出在满足这些要求的情况下可以组建的委员会的数量。

问题4

Ana、Bob 和 Cao 分别以$8.6$每秒米、$6.2$每秒米和$5$每秒米的恒定速度骑行。他们同时从一个矩形田野的东北角出发，田野的长边朝正西方向。Ana 开始沿着田野边缘骑行，最初向西行驶，Bob 开始沿着田野边缘骑行，最初向南行驶，而 Cao 则沿直线穿过田野骑行到$D$田野南边的某个点。Cao 到达点的时间$D$与 Ana 和 Bob 第一次到达 的时间相同$D$。田野的长度与宽度与从点$D$到田野东南角的距离之比可以表示为$p:q:r$，其中$p$、$q$和$r$是正整数$p$，且$q$互质。求$p+q+r$。

问题5

在附图中，外层正方形的$S$边长为。在内部构造$40$一个$S'$边长为 的正方形，其中心与 相同，边与 的边平行。从 边的每个中点向 的两个最近顶点画线段。结果是一个内接于 的四角星形图形。将星形图形剪下来，然后折叠成一个底面为 的金字塔。求这个金字塔的体积。 $15$$S$$S$$S$$S$$S'$$S$$S'$

[asy] 对 S1 = (20, 20), S2 = (-20, 20), S3 = (-20, -20), S4 = (20, -20); 对 M1 = (S1+S2)/2, M2 = (S2+S3)/2, M3=(S3+S4)/2, M4=(S4+S1)/2; 对 Sp1 = (7.5, 7.5), Sp2=(-7.5, 7.5), Sp3 = (-7.5, -7.5), Sp4 = (7.5, -7.5); 绘制(S1--S2--S3--S4--循环); 绘制(Sp1--Sp2--Sp3--Sp4--循环); 绘制(Sp1--M1--Sp2--M2--Sp3--M3--Sp4--M4--循环); [/asy]

问题 6

设$z=a+bi$为复数$\vert z \vert = 5$，且使得和$b>0$之间的距离最大化，且 令。求。 $(1+2i)z^3$$z^5$$z^4 = c+di$$c+d$

问题 7

设$S$为正整数的递增序列，其二进制表示恰好为$8$1。设$N$为 中的第 1000 个数字$S$。求$N$除以时的余数$1000$。

问题 8

复数$z$和$w$满足系统\[z + \frac{20i}w = 5+i\]\[w+\frac{12i}z = -4+10i\]求的最小可能值$\vert zw\vert^2$。

问题 9

设$x$和$y$为实数，且$\frac{\sin x}{\sin y} = 3$和$\frac{\cos x}{\cos y} = \frac12$。的值$\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y}$可以表示为形式$\frac pq$，其中$p$和$q$为互质正整数。求$p+q$。

问题 10

$n$找出小于的正整数的数量$1000$，使得存在一个正实数，$x$使得$n=x\lfloor x \rfloor$。

注意：$\lfloor x \rfloor$是小于或等于 的最大整数$x$。

问题11

设$f_1(x) = \frac23 - \frac3{3x+1}$，且对于$n \ge 2$，定义。满足$f_n(x) = f_1(f_{n-1}(x))$的值可以表示为 的形式，其中和是互质正整数。求。 $x$$f_{1001}(x) = x-3$$\frac mn$$百万$$n$$m+n$

问题 12

对于正整数，如果 的绝对值与的所有倍数相差大于，则$p$定义该正整数$n$为$p$-安全。例如，-安全数字集为。找出小于或等于 的正整数的数量，这些正整数同时为-安全、-安全和-安全。 $n$$2$$p$$10$$\{ 3, 4, 5, 6, 7, 13, 14, 15, 16, 17, 23, \ldots\}$$10,000$$7$$11$$13$

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2012年 AIME I 数学邀请赛真题和答案解析

2012年 AIME I 数学邀请赛真题

问题 1

求出具有三个不一定不同的数字的正整数的数量，$abc$其中和$a \neq 0$，并且和$c \neq 0$都是的倍数。 $abc$$cba$$4$

问题 2

等差数列的项加起来为$715$。数列的第一项增加$1$，第二项增加$3$，第三项增加$5$，一般来说，$k$第 项增加$k$第 奇数个正整数。新数列的项加起来为$836$。求原数列第一项、最后一项和中间项的和。

问题 3

九个人坐下来吃饭，有三种餐点可供选择。三个人点了牛肉餐，三个人点了鸡肉餐，三个人点了鱼肉餐。服务员以随机顺序提供九种餐点。求出服务员为九个人提供餐点的方式数量，使得只有一个人收到他点的餐点。

问题4

布奇和桑德斯需要离开道奇。为了尽快出发，他们轮流步行和骑着他们唯一的马斯帕基，如下所示。布奇先步行，桑德斯骑马。当桑德斯到达沿途每隔一英里就有一个拴马桩时，他把斯帕基拴在桩上，然后开始步行。布奇到达斯帕基时，他骑马直到经过桑德斯，然后在下一个拴马桩留下斯帕基，继续步行，就这样继续下去。斯帕基、布奇和桑德斯的步行速度分别为$6,$ $4,$和$2.5$英里每小时。布奇和桑德斯第一次在里程碑处相遇时，他们$n$距离道奇有数英里，并且已经旅行了$t$几分钟。求$n + t$。

问题5

设是所有可以用零和一（允许前导零）$B$书写的二进制整数的集合。如果执行所有可能的减法，其中一个元素从另一个元素中减去，求出得到 答案的次数。$5$$8$$B$$1$

问题 6

复数$z$和$w$满足$z^{13} = w,$ $w^{11} = z,$，且的虚部为$z$，$\sin{\frac{m\pi}{n}}$对于互质正整数$百万$，$n$且$m<n.$查找$n.$

问题 7

下图网络中的 16 个圆圈中，每个圆圈旁边都站着一名学生。16$3360$名学生共分配了 100 枚硬币。所有学生同时将相同数量的硬币传递给网络中的每位邻居，从而将所有硬币赠送出去。交易后，所有学生的硬币数量与开始时相同。求出站在中心圆圈的学生最初拥有的硬币数量。

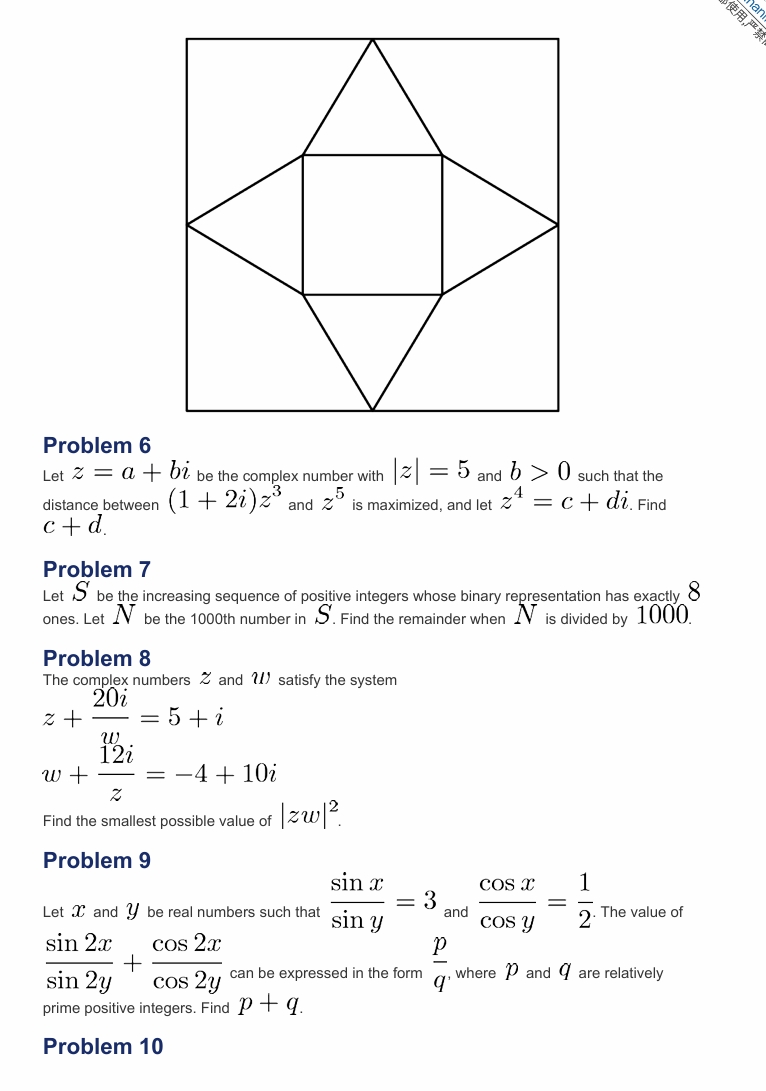
[asy] 导入cse5；单位尺寸（6mm）；默认笔（线宽（.8pt））；点因子 = 8；路径笔=黑色；对 A = (0,0)；对 B = 2*dir(54)，C = 2*dir(126)，D = 2*dir(198)，E = 2*dir(270)，F = 2*dir(342)；对 G = 3.6*dir(18)，H = 3.6*dir(90)，I = 3.6*dir(162)，J = 3.6*dir(234)，K = 3.6*dir(306)；对 M = 6.4*dir(54)，N = 6.4*dir(126)，O = 6.4*dir(198)，P = 6.4*dir(270)，L = 6.4*dir(342)；对[]点状 = {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P};D(A--B--H-- M); D(A--C--H--N); D(A--F--G--L); D(A--E--K--P); D(A-- D--J--O); D(B--G--M); D(F--K--L); D(E--J--P); D(O--I-- D); D(C--I--N​​); D(L--M--N--O--P--L); 点（虚线）；[/asy]

问题 8

$ABCDEFGH,$如下所示的立方体，其边长为，被一个通过顶点和中点和的$1$平面切割。该平面将立方体分成两个立体。两个立体中较大立体的体积可以写成如下形式，其中和是互质正整数。求$D$$M$$N$$\overline{AB}$$\overline{CG}$$\tfrac{p}{q},$$p$$q$$p+q.$

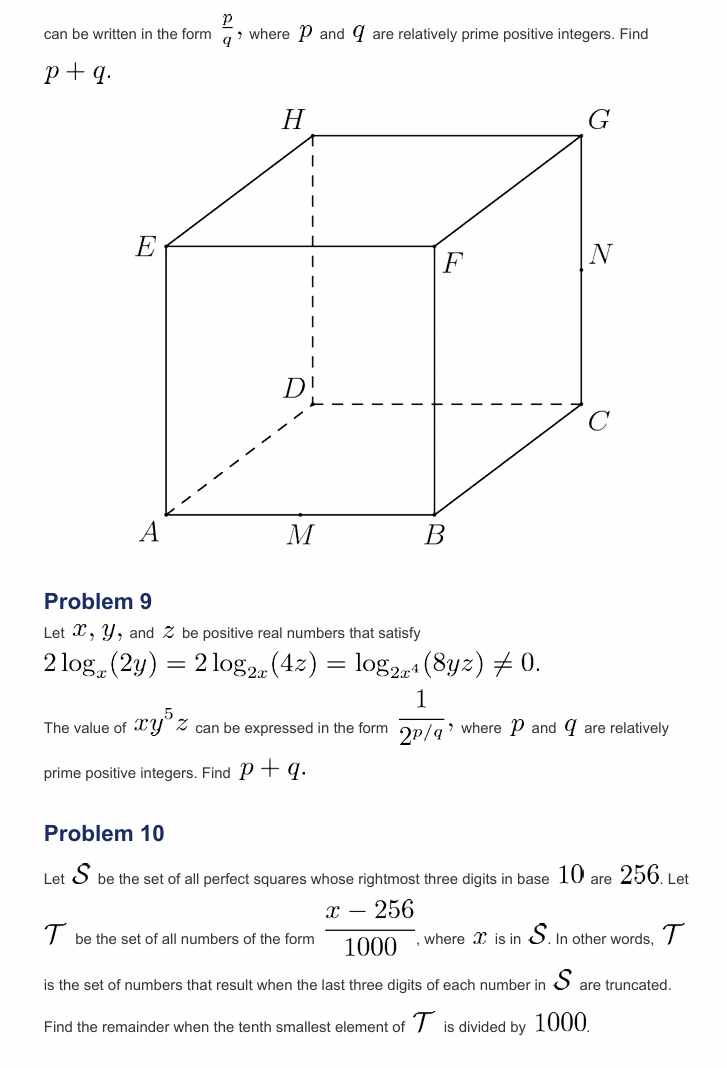
[asy]import cse5; unitize(10mm); pathpen=black; dotfactor=3; pair A = (0,0), B = (3.8,0), C = (5.876,1.564), D = (2.076,1.564), E = (0,3.8), F = (3.8,3.8), G = (5.876,5.364), H = (2.076,5.364), M = (1.9,0), N = (5.876,3.465); pair[] dotted = {A,B,C,D,E,F,G,H,M,N}; D(A--B--C--G--H--E--A); D(E--F--B); D(F--G); pathpen=dashed; D(A--D--H); D(D--C); dot(dotted);标签（“$A$”，A，SW）；标签（“$B$”，B，S）；标签（“$C$”，C，SE）；标签（“$D$”，D，NW）；标签（“$E$”，E，W）；标签（“$F$”，F，SE）；标签（“$G$”，G，NE）；标签（“$H$”，H，NW）；标签（“$M$”，M，S）；标签（“$N$”，N，NE）； [/asy]

问题 9

设$x,$ $y,$和$z$为满足的正实数，\[2\log_{x}(2y) = 2\log_{2x}(4z) = \log_{2x^4}(8yz) \ne 0.\]的值$xy^5z$可以表示为其中$\frac{1}{2^{p/q}},$和$p$为$q$互质正整数。求$p+q.$

问题 10

设$\mathcal{S}$为底数最右边三位为 的所有完全平方数的集合$10$。$256$设$\mathcal{T}$为所有形式为 的数的集合$\frac{x-256}{1000}$，其中$x$为 中的$\mathcal{S}$。换句话说，$\mathcal{T}$是截断 中每个数的后三位后所得的数的集合$\mathcal{S}$。求 的第十小元素$\mathcal{T}$除以后的余数$1000$。

问题11

一只青蛙从 开始$P_0 = (0,0)$，按照以下规则进行一系列跳跃：从 开始，$P_n = (x_n, y_n),$青蛙跳到 ，$P_{n+1},$可以是 中的任何点$（x_n + 7，y_n + 2），$ $（x_n + 2，y_n + 7），$ $（x_n-5，y_n-10），$或$(x_n - 10，y_n - 5).$有$M$点可以通过一系列这样的跳跃到达。当 除以 时，求$(x, y)$余数$|x| + |y| ≤ 100$$M$1000 美元

问题 12

设$\三角形ABC$是直角三角形，直角位于 设$C.$和$D$是$E$上的点，$\overline{AB}$位于和$D$之间，使得和三等分如果则可写成 其中和是互质正整数，并且是不能被任何素数的平方整除的正整数。求$A$$E$$\overline{CD}$$\overline{CE}$$\角度C.$$\frac{DE}{BE} = \frac{8}{15},$$\tan B$$\frac{m \sqrt{p}}{n},$$百万$$n$$p$$m+n+p.$

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2013年 AIME II 数学邀请赛真题和答案解析

2013年 AIME II 数学邀请赛真题

问题 1

假设将一天的时间测量转换为公制，这样每天有$10$公制小时，每个公制小时有$100$公制分钟。然后就可以生产出可以$\text{9:99}$在午夜前、$\文本{0:00}$午夜时、上午$\text{1:25}$前$\text{3:00}$和$\text{7:50}$下午前读数的数字时钟$\text{6:00}$。转换后，想要在上午前醒来的人$\text{6:36}$可以将他的新数字闹钟设置为$\text{A:BC}$，其中$\text{A}$，$\text{B}$和$\text{C}$是数字。求$100\text{A}+10\text{B}+\text{C}$。

问题 2

正整数$a$，并$b$满足条件\[\log_2(\log_{2^a}(\log_{2^b}(2^{1000}))) = 0.\]求出所有可能值的总和$a+b$。

问题 3

一根大蜡烛$119$高 厘米。它被设计成在刚点燃时燃烧得更快，在接近底部时燃烧得更慢。具体来说，蜡烛$10$从顶部燃烧第一厘米需要 秒，$20$燃烧第二厘米需要 秒，$10,000$燃烧第 - 厘米需要 秒。假设蜡烛完全燃烧$k$需要秒。那么点燃后几秒，蜡烛的高度（以厘米为单位）为。求。 $T$$\tfrac{T}{2}$$h$$10小时$

问题4

在笛卡尔平面中设$A = (1,0)$和。构造$B = \left( 2, 2\sqrt{3} \right)$等边三角形，使得位于第一象限。设是的中心。则可写成，其中和是互质正整数，是不能被任何素数的平方整除的整数。求。 $ABC$加元$P=(x,y)$$\三角形ABC$$x \cdot y$$\tfrac{p\sqrt{q}}{r}$$p$$r$$q$$p+q+r$

问题5

在等边形中$\三角形ABC$设点$D$和$E$三等分$\overline{BC}$。则可$\sin(\angle DAE)$表示为形式$\frac{a\sqrt{b}}{c}$，其中$a$和$c$为互质正整数，为$b$不能被任何素数的平方整除的整数。求$a+b+c$。

问题 6

寻找最小正整数，使得以 开头的连续整数$N$集不包含整数的平方。 $1000$$1000\cdot N$

问题 7

一组办事员被分配了整理文件的任务$1775$。每个办事员每小时以恒定的速度整理$30$文件。在第一个小时结束时，一些办事员被重新分配到另一项任务；在第二个小时结束时，相同数量的剩余办事员也被重新分配到另一项任务，在第三个小时结束时也会进行类似的分配。该组在$3$几小时和$10$几分钟内完成了整理工作。求在第一个半小时内整理的文件数量。

问题 8

一个内接于圆的六边形的边长依次为$22$、$22$、$20$、$22$、$22$和$20$。圆的半径可以写成$p+\sqrt{q}$，其中$p$和$q$为正整数。求$p+q$。

问题 9

棋盘上$7\乘以 1$完全铺满了$m\times 1$没有重叠的瓷砖；每块瓷砖可以覆盖任意数量的连续方格，每块瓷砖都完全位于棋盘上。每块瓷砖要么是红色的，要么是蓝色的，要么是绿色的。设$N$为棋盘上至少使用过一次三种颜色的瓷砖的数量$7\乘以 1$。例如，$1\乘以 1$红色瓷砖后面跟着$2\乘以 1$绿色瓷砖、$1\乘以 1$绿色瓷砖、$2\乘以 1$蓝色瓷砖和$1\乘以 1$绿色瓷砖，这是有效的瓷砖。请注意，如果$2\乘以 1$用两个蓝色瓷砖替换蓝色瓷砖$1\乘以 1$，则会导致不同的瓷砖。当$N$除以时，求余数$1000$。

问题 10

给定一个半径为 的圆$\sqrt{13}$，设$A$为距圆心 的点$4 + \sqrt{13}$。$O$设$B$为圆上离点 最近的点$A$。过该点的直线与$A$圆相交于点$K$和$L$。 的最大可能面积$\三角形BKL$可以写成 的形式$\frac{a - b\sqrt{c}}{d}$，其中$a$、$b$、$c$和$d$为正整数，$a$且$d$为互质，且不$c$能被任何质数的平方整除。求$a+b+c+d$。

问题11

设，设为集合中函数​​的个数，使得$A = \{1, 2, 3, 4, 5, 6, 7\}$为常数函数。求除以时的余数。 $N$$f$$A$$A$$f(f(x))$$N$$1000$

问题 12

设$S$为所有形式为 的多项式的集合$z^3 + az^2 + bz + c$，其中$a$、$b$和$c$为整数。求出 中的多项式个数$S$，使得其每个根$z$满足$|z| = 20$或$|z| = 13$。

问题 13

在 中$\三角形ABC$， ，且上的$AC = BC$点为 ，使得 。设为 的中点。已知和， 的面积可表示为 的形式，其中和为正整数，且不能被任何素数的平方整除。求。 $D$$\overline{BC}$$CD = 3\cdot BD$$E$$\overline{AD}$$CE = \sqrt{7}$$BE = 3$$\三角形ABC$$m\sqrt{n}$$百万$$n$$n$$m+n$

问题14

对于正整数$n$和$k$，设为除以$f(n, k)$时的余数，设为。求除以时的余数。 $n$$k$$n> 1$$F(n) = \max_{\substack{1\le k\le \frac{n}{2}}} f(n, k)$$\sum\limits_{n=20}^{100} F(n)$$1000$

问题15

设$A,B,C$是锐角三角形的内角，\begin{align*} \cos^2 A + \cos^2 B + 2 \sin A \sin B \cos C &= \frac{15}{8} \text{ 和} \\ \cos^2 B + \cos^2 C + 2 \sin B \sin C \cos A &= \frac{14}{9} \end{align*}有正整数$p$，，，和，其中和互质，$q$不能被任何质数的平方整除。求。 $r$$s$\[\cos^2 C + \cos^2 A + 2 \sin C \sin A \cos B = \frac{pq\sqrt{r}}{s},\]$p+q$$s$$r$$p+q+r+s$

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2013年 AIME I 数学邀请赛真题和答案解析

2013年 AIME I 数学邀请赛真题

问题 1

AIME 铁人三项赛包括半英里游泳、30 英里自行车骑行和八英里跑步。汤姆以恒定的速度游泳、骑自行车和跑步。他的跑步速度是游泳速度的五倍，骑自行车的速度是跑步速度的两倍。汤姆在四个半小时内完成了 AIME 铁人三项赛。他骑自行车花了多少分钟？

问题 2

$n$求出满足以下条件的 五位正整数的数量：

（a）该数字$n$可以被整除$5,$（b）的首位数字和末位数字$n$相等，并且（c） 的数字$n$之和可以被整除5 美元

问题 3

设$ABCD$是一个正方形，设和$E$分别是和$F$上的点。过平行线和过平行线的线将正方形分成两个正方形和两个非正方形的矩形。两个正方形的面积之和为正方形的面积求$\overline{AB}$$\overline{BC},$$E$$\overline{BC}$$F$$\overline{AB}$$ABCD$$\frac{9}{10}$$ABCD.$$\frac{AE}{EB} + \frac{EB}{AE}.$

问题4

在下面显示的正方形数组中$13$，$8$正方形被涂成红色，其余$5$正方形被涂成蓝色。如果随机选择所有可能的颜色之一，则所选颜色数组在$90^{\circ}$围绕中心正方形旋转时出现相同的概率为$\frac{1}{n}$，其中$n$为正整数。求$n$。

[asy] 绘制((0,0)--(1,0)--(1,1)--(0,1)--(0,0)); 绘制((2,0)--(2,2)--(3,2)--(3,0)--(3,1)--(2,1)--(4,1)--(4,0)--(2,0)); 绘制((1,2)--(1,4)--(0,4)--(0,2)--(0,3)--(1,3)--(-1,3)--(-1,2)--(1,2)); 绘制((-1,1)--(-3,1)--(-3,0)--(-1,0)--(-2,0)--(-2,1)--(-2,-1)--(-1,-1)--(-1,1));绘制（（0，-1）--（0，-3）--（1，-3）--（1，-1）--（1，-2）--（0，-2）--（2，-2）--（2，-1）--（0，-1））；大小（100）；[/asy]

问题5

该方程的实数根$8x^3-3x^2-3x-1=0$可以写成 的形式$\frac{\sqrt[3]{a}+\sqrt[3]{b}+1}{c}$，其中$a$、$b$和$c$为正整数。求$a+b+c$。

问题 6

梅琳达有三个空盒子和$12$教科书，其中三本是数学教科书。一个盒子可以装她的任意三本教科书，一个盒子可以装她的任意四本教科书，一个盒子可以装她的任意五本教科书。如果梅琳达以随机顺序将她的教科书装入这些盒子，那么所有三本数学教科书最终都装在同一个盒子中的概率可以写成$\frac{m}{n}$，其中$百万$和$n$是互质正整数。求$m+n$。

问题 7

一个矩形盒子的宽度为$12$英寸，长度为$16$英寸，高度为$\frac{m}{n}$英寸，其中$百万$和$n$是互质正整数。盒子的三个面在盒子的一个角相交。这三个面的中心点是面积为$30$平方英寸的三角形的顶点。求$m+n$。

问题 8

函数的定义域$f(x) = \arcsin(\log_{m}(nx))$是长度为 的一个闭区间$\frac{1}{2013}$，其中$百万$和$n$为正整数和。求除以$m> 1$后的最小可能和的余数。 $m+n$$1000$

问题 9

一个纸质等边三角形，$ABC$边长为$12$。将纸质三角形折叠起来，使顶点与距离的$A$边上的一点相切。折叠三角形所沿的线段长度可以写成，其中、和为正整数，和互质，且不能被任何质数的平方整除。求。 $\overline{BC}$$9$$B$$\frac{m\sqrt{p}}{n}$$百万$$n$$p$$百万$$n$$p$$m+n+p$

[asy] 导入 cse5; 大小(12cm); 笔 tpen = defaultpen + 1.337; 实际 a = 39/5.0; 实际 b = 39/7.0; 对 B = MP("B", (0,0), dir(200)); 对 A = MP("A", (9,0), dir(-80)); 对 C = MP("C", (12,0), dir(-20)); 对 K = (6,10.392); 对 M = (a*B+(12-a)*K) / 12; 对 N = (b*C+(12-b)*K) / 12; 绘制(B--M--N--C--cycle, tpen); 绘制(M--A--N--cycle); 填充(M--A--N--cycle, mediumgrey); 对 shift = (-20.13, 0);对 B1 = MP("B", B+shift, dir(200)); 对 A1 = MP("A", K+shift, dir(90)); 对 C1 = MP("C", C+shift, dir(-20)); draw(A1--B1--C1--cycle, tpen);[/asy]

问题 10

有非零整数$a$、$b$、$r$和，$s$使得复数$r+si$是多项式的零点。对于和$P(x)={x}^{3}-a{x}^{2}+bx-65$的每种可能组合，设为 的零点之和。求和 的所有可能组合的 之和。 $a$$b$${p}_{a,b}$$P(x)$${p}_{a,b}$$a$$b$

问题11

Math 女士的幼儿园班级有$16$注册学生。教室里有非常多的积木，$N$满足以下条件：

（a）如果班上有 、 或 名学生，则在每种情况下，所有的积木都可以平等地分配给每个学生 $16$，$15$并且$14$

(b) 有三个整数$0<x<y<z<14$，当有$x$、$y$或 名$z$学生在场，并将积木数量相等地分配给每个学生时，恰好剩下三块积木。

$N$找出满足上述条件 的最小可能值的不同素因数的和。

问题 12

设$\bigtriangleup PQR$为三角形，$\角度 P = 75^o$且。在 内画$\角度 Q = 60^o$一个边长为 1 的正六边形，使 边位于 上， 边位于 上，其余顶点之一位于 上。有正整数和 ，使得 的面积可以表示为 的形式，其中和互质，且 c 不能被任何质数的平方整除。求。 $ABCDEF$$\三角PQR$$\overline{AB}$$\overline{PQ}$$\overline{CD}$$\overline{QR}$$\overline{RP}$$a,b,c,$$d$$\三角PQR$$\frac{a+b\sqrt{c}}{d}$$a$$d$$a+b+c+d$

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2014年 AIME II 数学邀请赛真题和答案解析

2014年 AIME II 数学邀请赛真题

问题 1

Abe 可以在 15 小时内粉刷完房间，Bea 的粉刷速度比 Abe 快 50%，而 Coe 的粉刷速度是 Abe 的两倍。Abe 开始粉刷房间，前一个半小时他独自工作。然后 Bea 加入 Abe，他们一起工作，直到粉刷完一半的房间。然后 Coe 加入 Abe 和 Bea，他们一起工作，直到粉刷完整个房间。求出 Abe 开始工作后他们三个人完成粉刷房间所需的分钟数。

问题 2

阿诺德正在研究男性群体中三个健康风险因素（分别表示为 A、B 和 C）的流行程度。对于这三个因素中的每一个，在群体中随机选择的一名男性只具有这一个风险因素（而没有其他风险因素）的概率为 0.1。对于这三个因素中的任意两个，随机选择的一名男性恰好具有这两个风险因素（但没有第三个风险因素）的概率为 0.14。假设一名随机选择的男性具有 A 和 B，则他同时具有所有三个风险因素的概率为$\frac{1}{3}$。假设一名男性没有风险因素 A，则他同时不具有这三个风险因素中的任何一个的概率为$\frac{p}{q}$，其中$p$和$q$是互质正整数。求$p+q$。

问题 3

一个矩形的边长为$a$和 36。在矩形的每个顶点以及每条边长为 36 的中点处都安装了一个铰链。$a$可以将长度为 的边压向彼此，使这两条边保持平行，这样矩形就变成了如图所示的凸六边形。当图形为六边形，且长度为 的边$a$平行且相距 24 时，六边形的面积与原始矩形相同。求$a^2$。

[asy] 对 A、B、C、D、E、F、R、S、T、X、Y、Z；dotfactor = 2；unitsize(.1cm)；A = (0,0);B = (0,18);C = (0,36);//不要看这里D = (12*2.236, 36);E = (12*2.236, 18);F = (12*2.236, 0);draw(A--B--C--D--E--F--cycle);dot(" ",A,NW);dot(" ",B,NW);dot(" ",C,NW);dot(" ",D,NW);dot(" ",E,NW);dot(" ",F,NW);//不要看这里R = (12*2.236 +22,0); S = (12*2.236 + 22 - 13.4164,12); T = (12*2.236 + 22,24); X = (12*4.472+ 22,24); Y = (12*4.472+ 22 + 13.4164,12); Z = (12*4.472+ 22,0); draw(R--S--T--X--Y--Z--cycle); dot(" ",R,NW); dot(" ",S,NW); dot(" ",T,NW); dot(" ",X,NW); dot(" ",Y,NW); dot(" ",Z,NW); // sqrt180 = 13.4164 // sqrt5 = 2.236[/asy]

问题4

循环小数$0.abab\overline{ab}$并$0.abcabc\overline{abc}$满足

$0.abab\overline{ab}+0.abcabc\overline{abc}=\frac{33}{37},$

其中$a$、$b$和$c$是（不一定是不同的）数字。求三位数$abc$。

问题5

实数$r$和$s$是的根$p(x)=x^3+ax+b$，而$r+4$和$s-3$是的根$q(x)=x^3+ax+b+240$。求出所有可能值的和$|b|$。

问题 6

查尔斯有两个六面骰子。其中一个骰子是公平的，另一个骰子有偏差，因此它出现六的概率为 ，$\frac{2}{3}$而其他五个面的概率均为$\frac{1}{15}$。查尔斯随机选择两个骰子中的一个并掷三次。假设前两次掷出的都是六，那么第三次掷出的也是六的概率为$\frac{p}{q}$，其中$p$和$q$是互质正整数。求$p+q$。

问题 7

设$f(x)=(x^2+3x+2)^{\cos(\pi x)}$。求出所有正整数的和，$n$满足 $\left |\sum_{k=1}^n\log_{10}f(k)\right|=1.$

问题 8

半径加元为2的圆直径为$\overline{AB}$。圆$D$在 处内切于圆加元。$A$圆$E$内切于圆加元，外切于圆$D$，并切于$\overline{AB}$。圆的半径$D$是圆 半径的三倍$E$，可以写成 的形式$\sqrt{m}-n$，其中$百万$和$n$为正整数。求$m+n$。

问题 9

十把椅子围成一圈。求这组椅子中至少包含三把相邻椅子的子集的数量。

问题 10

设$z$为复数，且。 $|z|=2014$设$P$为复平面上的多边形，其顶点为 ，$z$且 ，$w$使得$\frac{1}{z+w}=\frac{1}{z}+\frac{1}{w}$。则 所围面积$P$可写成 的形式$n\sqrt{3}$，其中$n$为整数。求$n$除以后的余数。$1000$

问题11

在 中$\triangle 红色$，$\measuredangle DRE=75^{\circ}$且$\measuredangle RED=45^{\circ}$。$RD=1$设$M$为线段 的中点$\overline{RD}$。点加元位于 边，$\overline{ED}$使得$\overline{RC}\perp\overline{EM}$。延伸线段$\overline{DE}$至$E$点，$A$使得$CA=AR$。则$AE=\frac{a-\sqrt{b}}{c}$，其中$a$和$c$为互质正整数，且$b$为正整数。求$a+b+c$。

问题 12

假设 的角$\三角形ABC$满足$\cos(3A)+\cos(3B)+\cos(3C)=1$。三角形的两条边的长度分别为 10 和 13。存在一个正整数$百万$，使得 剩余一条边的最大可能长度为$\三角形ABC$。$\sqrt{m}$求$百万$。

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓

2014年 AIME I 数学邀请赛真题和答案解析

2014年 AIME I 数学邀请赛真题和答案解析

问题 1

运动鞋鞋带的 8 个鞋眼都位于一个矩形上，长边上各有 4 个鞋眼，间距相等。矩形宽 50 毫米，长 80 毫米。矩形的每个顶点都有一个鞋眼。鞋带本身必须沿着矩形的一条宽边穿过顶点鞋眼，然后在连续的鞋眼之间交叉，直到到达矩形另一条宽边的两个鞋眼，如图所示。穿过最后的鞋眼后，鞋带的每一端必须延伸至少 200 毫米，以便打结。求出鞋带的最小长度（以毫米为单位）。

[asy] 尺寸（200）；默认笔（线宽（0.7））；路径 laceL=（-20，-30）..张力 0.75 ..（-90，-135）..（-102，-147）..（-152，-150）..张力 2 ..（-155，-140）..（-135，-40）..（-50，-4）..张力 0.8 ..原点；路径 laceR=reflect（（75,0），（75，-240））*laceL；绘制（原点--（0，-240）--（150，-240）--（150,0）--循环，灰色）； for(int i=0;i<=3;i=i+1) { path circ1=circle((0,-80*i),5),circ2=circle((150,-80*i),5); unfill(circ1); draw(circ1); unfill(circ2); draw(circ2); } draw(laceL--(150,-80)--(0,-160)--(150,-240)--(0,-240)--(150,-160)--(0,-80)--(150,0)^^laceR,linewidth(1));[/asy]

问题 2

一个瓮里有$4$绿球和$6$蓝球。另一个瓮里有$16$绿球和$N$蓝球。从每个瓮中随机抽取一个球。两个球颜色相同的概率是$0.58$。求$N$。

问题 3

求有理数的数量$r$，$0<r<1,$当$r$写成最低项的分数时，分子与分母的和为$1000$。

问题4

乔恩和史蒂夫沿着一条与东西方向两条并排的火车轨道平行的路径骑自行车。乔恩以$20$每小时英里的速度向东骑行，史蒂夫以$20$每小时英里的速度向西骑行。两列长度相等的火车以恒定但不同的速度向相反的方向行驶，每列火车都经过这两名乘客。每列火车经过$1$乔恩的时间恰好是分钟。西行的火车经过$10$史蒂夫的时间与东行的火车一样长。每列火车的长度为$\tfrac{m}{n}$英里，其中$百万$和$n$是互质正整数。求$m+n$。

问题5

假设集合$S = \{P_1, P_2, \dots, P_{12}\}$由一个正边形的十二个顶点组成$12$。如果存在一个圆，使得 的所有点都在圆内，而 的所有不在圆内的点都在圆外，则$Q$的子集被称为公有子集。有多少个公有子集？（请注意，空集是公有子集。） $S$$Q$$S$$Q$

问题 6

图$y = 3(xh)^2 + j$和的$y = 2(xh)^2 + k$y 截距分别为$2013$和$2014$，且每个图都有两个正整数 x 截距。求$h$。

问题 7

设$w$和$z$为复数，且$|w| = 1$和$|z| = 10$。设$\theta = \arg \left(\tfrac{wz}{z}\right)$。的最大可能值$\tan^2 \theta$可以写成$\tfrac{p}{q}$，其中$p$和$q$是互质正整数。求$p+q$。（注意$\arg(w)$，对于，表示从到$w \neq 0$的射线与复平面中的正实轴所成的角度的度数。） $0$$w$

问题 8

正整数$N$和以十进制表示时，$N^2$结尾都是相同的四位数序列，其中数字不为零。求三位数。 $abcd$$a$$abc$

问题 9

设$x_1<x_2<x_3$是方程的三个实根$\sqrt{2014} x^3 - 4029x^2 + 2 = 0$。求$x_2(x_1+x_3)$。

问题 10

半径为 的圆盘与$1$半径为 的圆盘外切$5$。设$A$为圆盘切点，加元为小圆盘中心，$E$为大圆盘中心。大圆盘保持不动，小圆盘可以沿大圆盘外侧滚动，直到小圆盘旋转 的角度。$360^\circ$也就是说，如果小圆盘中心移动到点$D$，小圆盘上从 开始的点$A$现在移动到点$B$，则$\overline{AC}$平行于$\overline{BD}$。然后$\sin^2(\angle BEA)=\tfrac{m}{n}$，其中$百万$和$n$是互质正整数。求$m+n$。

问题11

$(0,0)$一个标记从 - 坐标网格的点开始$xy$，然后进行六次移动。每次移动都是在与其中一个坐标轴平行的方向上移动 1 个单位。每次移动都是从四个可能的方向中随机选择的，并且与其他移动无关。标记在图形上某个点结束的概率$|y|=|x|$是$\tfrac{m}{n}$，其中$百万$和$n$是互质正整数。求$m+n$。

问题 12

设$A=\{1,2,3,4\}$，和$f$和是从到$g$随机选取的（不一定不同）函数。 的范围和 的范围不相交的概率为，其中和是互质正整数。求。 $A$$A$$f$$g$$\tfrac{m}{n}$$百万$$n$$百万$

问题 13

在正方形 上$ABCD$，点$E,F,G$、 和分别$H$位于边$\overline{AB},\overline{BC},\overline{CD},$和 上$\overline{DA},$，使得$\overline{EG} \perp \overline{FH}$和$EG=FH = 34$。线段$\overline{EG}$和$\overline{FH}$相交于点，四边形和$P$的面积比为求正方形 的面积。 $AEPH、BFPE、CGPF,$$DHPG$$269:275:405:411.$$ABCD$

[asy] 对 A = (0,sqrt(850));对 B = (0,0)；对 C = (sqrt(850),0);对 D = (sqrt(850),sqrt(850));绘制（A--B--C--D--循环）；点因子 = 3；点(“$A$”,A,dir(135));点(“$B$”,B,dir(215));点(“$C$”,C,dir(305));点(“$D$”,D,dir(45));对 H = ((2sqrt(850)-sqrt(306))/6,sqrt(850));对 F = ((2sqrt(850)+sqrt(306)+7)/6,0);点(“$H$”,H,dir(90));点（“$F$”，F，dir（270））；绘制（H--F）；对 E = (0，（sqrt（850）-6）/2）；对 G = (sqrt（850） ,(sqrt(850)+sqrt(100))/2); 点("$E$",E,dir(180)); 点("$G$",G,dir(0)); 绘制( E--G); 对 P = 扩展（H，F，E，G）； 点（“$P$”，P，dir（60））； 标签（“$w$”， 交点（A--P , E--H )); 标签("$x$", 交点( B--P, E--F )); 标签("$y$", 交点( C--P, G--F ) ); 标签("$z$", 交点( D--P, G--H ));[/asy]

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓