2012年 AIME II 数学邀请赛真题
问题 1
![]() 求出方程的正整数解的有序对的数量
求出方程的正整数解的有序对的数量![]() 。
。
问题 2
两个等比数列![]() 和
和![]() 有相同的公比,即
有相同的公比,即![]() ,,
,,![]() 和
和![]() 。求
。求![]() 。
。
问题 3
某大学数学系下设数学系、统计学系和计算机科学系,每个系有两名男教授和两名女教授,一个由六名教授组成的委员会应包含三名男教授和三名女教授,并且还必须包含来自三个系的两名教授。求出在满足这些要求的情况下可以组建的委员会的数量。
问题4
Ana、Bob 和 Cao 分别以![]() 每秒米、
每秒米、![]() 每秒米和
每秒米和![]() 每秒米的恒定速度骑行。他们同时从一个矩形田野的东北角出发,田野的长边朝正西方向。Ana 开始沿着田野边缘骑行,最初向西行驶,Bob 开始沿着田野边缘骑行,最初向南行驶,而 Cao 则沿直线穿过田野骑行到
每秒米的恒定速度骑行。他们同时从一个矩形田野的东北角出发,田野的长边朝正西方向。Ana 开始沿着田野边缘骑行,最初向西行驶,Bob 开始沿着田野边缘骑行,最初向南行驶,而 Cao 则沿直线穿过田野骑行到![]() 田野南边的某个点。Cao 到达点的时间
田野南边的某个点。Cao 到达点的时间![]() 与 Ana 和 Bob 第一次到达 的时间相同
与 Ana 和 Bob 第一次到达 的时间相同![]() 。田野的长度与宽度与从点
。田野的长度与宽度与从点![]() 到田野东南角的距离之比可以表示为
到田野东南角的距离之比可以表示为![]() ,其中
,其中![]() 、
、![]() 和
和![]() 是正整数
是正整数![]() ,且
,且![]() 互质。求
互质。求![]() 。
。
问题5
在附图中,外层正方形的![]() 边长为。在内部构造
边长为。在内部构造![]() 一个
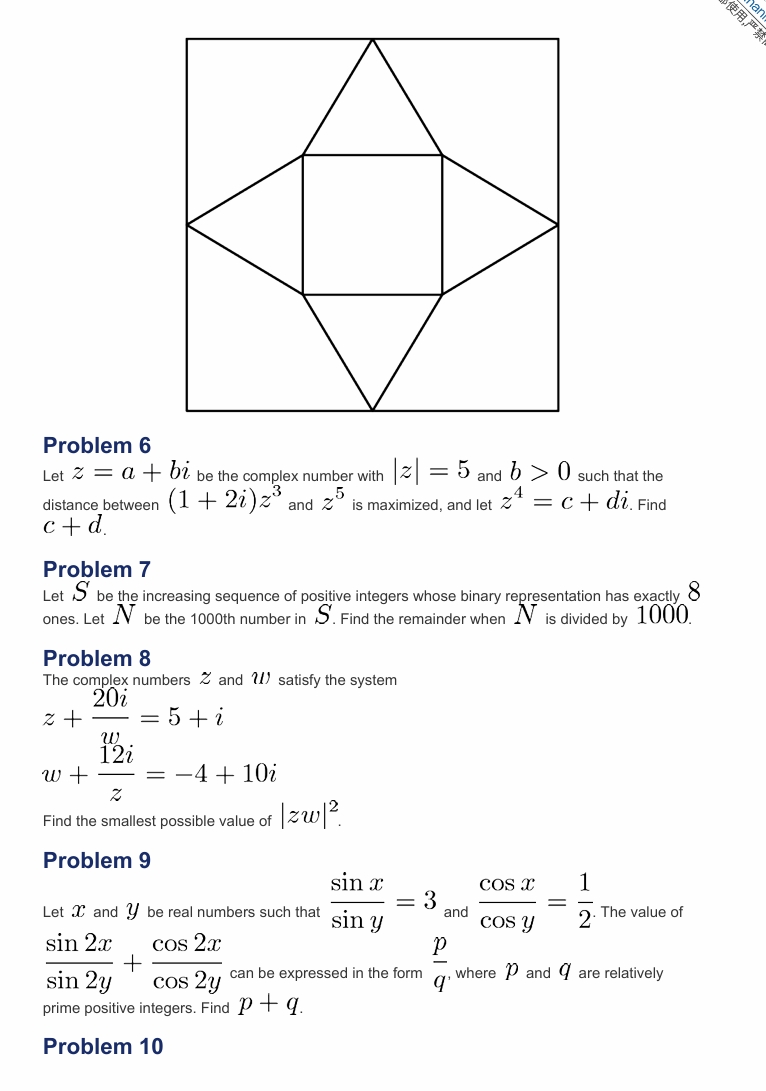
一个![]() 边长为 的正方形,其中心与 相同,边与 的边平行。从 边的每个中点向 的两个最近顶点画线段。结果是一个内接于 的四角星形图形。将星形图形剪下来,然后折叠成一个底面为 的金字塔。求这个金字塔的体积。
边长为 的正方形,其中心与 相同,边与 的边平行。从 边的每个中点向 的两个最近顶点画线段。结果是一个内接于 的四角星形图形。将星形图形剪下来,然后折叠成一个底面为 的金字塔。求这个金字塔的体积。 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[asy] 对 S1 = (20, 20), S2 = (-20, 20), S3 = (-20, -20), S4 = (20, -20); 对 M1 = (S1+S2)/2, M2 = (S2+S3)/2, M3=(S3+S4)/2, M4=(S4+S1)/2; 对 Sp1 = (7.5, 7.5), Sp2=(-7.5, 7.5), Sp3 = (-7.5, -7.5), Sp4 = (7.5, -7.5); 绘制(S1--S2--S3--S4--循环); 绘制(Sp1--Sp2--Sp3--Sp4--循环); 绘制(Sp1--M1--Sp2--M2--Sp3--M3--Sp4--M4--循环); [/asy]](https://latex.artofproblemsolving.com/2/8/6/2862b9fac9f2c88c10b30e3908cf4ac1d5f62115.png)
问题 6
设![]() 为复数
为复数![]() ,且使得和
,且使得和![]() 之间的距离最大化,且 令。求。
之间的距离最大化,且 令。求。 ![]()
![]()
![]()
![]()
问题 7
设![]() 为正整数的递增序列,其二进制表示恰好为
为正整数的递增序列,其二进制表示恰好为![]() 1。设
1。设![]() 为 中的第 1000 个数字
为 中的第 1000 个数字![]() 。求
。求![]() 除以时的余数
除以时的余数![]() 。
。
问题 8
复数![]() 和
和![]() 满足系统
满足系统![]()
![]() 求的最小可能值
求的最小可能值![]() 。
。
问题 9
设![]() 和
和![]() 为实数,且
为实数,且![]() 和
和![]() 。的值
。的值![]() 可以表示为形式
可以表示为形式![]() ,其中
,其中![]() 和
和![]() 为互质正整数。求
为互质正整数。求![]() 。
。
问题 10
![]() 找出小于的正整数的数量
找出小于的正整数的数量![]() ,使得存在一个正实数,
,使得存在一个正实数,![]() 使得
使得![]() 。
。
注意:![]() 是小于或等于 的最大整数
是小于或等于 的最大整数![]() 。
。
问题11
设![]() ,且对于
,且对于![]() ,定义。满足
,定义。满足![]() 的值可以表示为 的形式,其中和是互质正整数。求。
的值可以表示为 的形式,其中和是互质正整数。求。 ![]()
![]()
![]()
![]()
![]()
![]()
问题 12
对于正整数,如果 的绝对值与的所有倍数相差大于,则![]() 定义该正整数
定义该正整数![]() 为
为![]() -安全。例如,-安全数字集为。找出小于或等于 的正整数的数量,这些正整数同时为-安全、-安全和-安全。
-安全。例如,-安全数字集为。找出小于或等于 的正整数的数量,这些正整数同时为-安全、-安全和-安全。 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
以下是我们为您整理的全英版pdf真题:


扫码免费获取完整版真题+解析~~~
还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓



