本页面介绍了AIME考试形式、AIME详细考察范围、AIME与AMC10/12考试内容有何异同、AMC10/12晋级AIME需要补充的知识点、近两年 AIME I 试题分析、AIME竞赛难度体现在哪。
一、AIME考试形式是什么?
有15个开放式问题(填空题);每个问题的答案都是一个三位数的正整数,从000、001......直到 999;考试时间为3个小时;它们涵盖代数、几何、数论和组合学,展示了卓越数学所需的各种技能。
二、AIME竞赛详细考察范围是什么?
AIME和AMC 10、AMC 12一样,考查范围仍然是算术、代数、计数、几何、数论和概率(微积分不在数学竞赛考查范围内),但允许使用微积分方法解题。
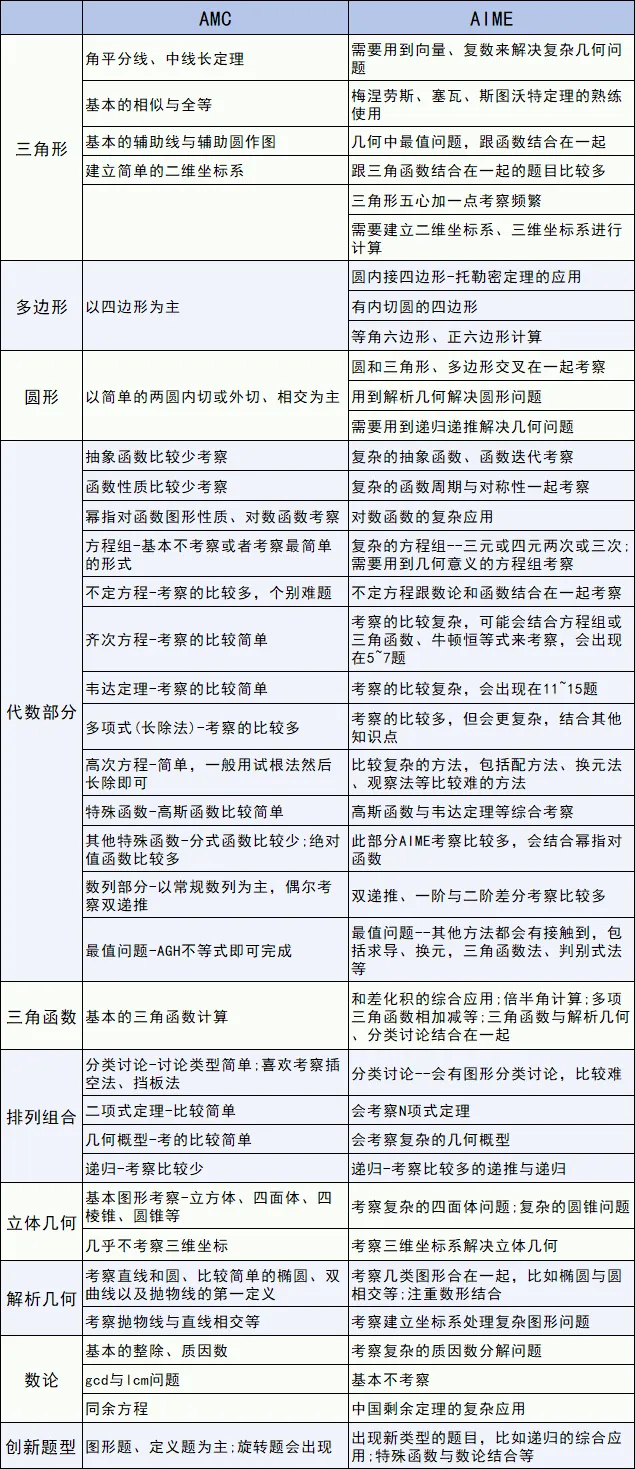
AIME竞赛基本内容
| 代数 | 多项式:代数基本定理、因式定理、余式定理、拉格朗日插值公式、*多安式的差分、*整值多项式 |
| 对数、复数与三角函数:对数、复数与三角函数的基本运算,单位根,复数的几何意义及应用,与复数相关的方程问题 | |
| 数列:通项公式、常系数线性递推数列、数列求和、数列不等式 | |
| 不等式:均值不等式、柯西不等式、排序不等式、各类最值问题 | |
| 几何 | 直线型:Menelauss定理、Ceva定理、Stewart定理、面积问题与面积方法正弦定理、余弦定理 |
| 圆:三角形的五心、四点共圆、Ptolemy定理、圆幕定理、根轴与根心 | |
| 立体几何:立体图形的体积计算、内切球与外接球、立体几何综合问题 | |
| 解析几何:平面与空间解析几何及其应用 | |
| 组合 | 排列组合:二项式定理、组合恒等式初步、映射方法、容斥原理、递推方法经典组合计数模型 |
| 概率:古典概型、几何概型、条件概率、Bayes公式、概率期望 | |
| 数论 | 基础:整除、同余、算术基本定理、最大公约数与最小公约数、辗转相除法、Bezout等式、取整函数、勒让德公式 |
| 著名数学定理:Fermat小定理、Wilson定理、中国剩余定理、阶的性质及应用LTE引理 | |
| 不定方程:线性不定方程、勾股方程、二次方程的整数根、代数变形解不定方程、同余分析解不定方程 |
三、AIME与AMC10/12考试内容有何异同?
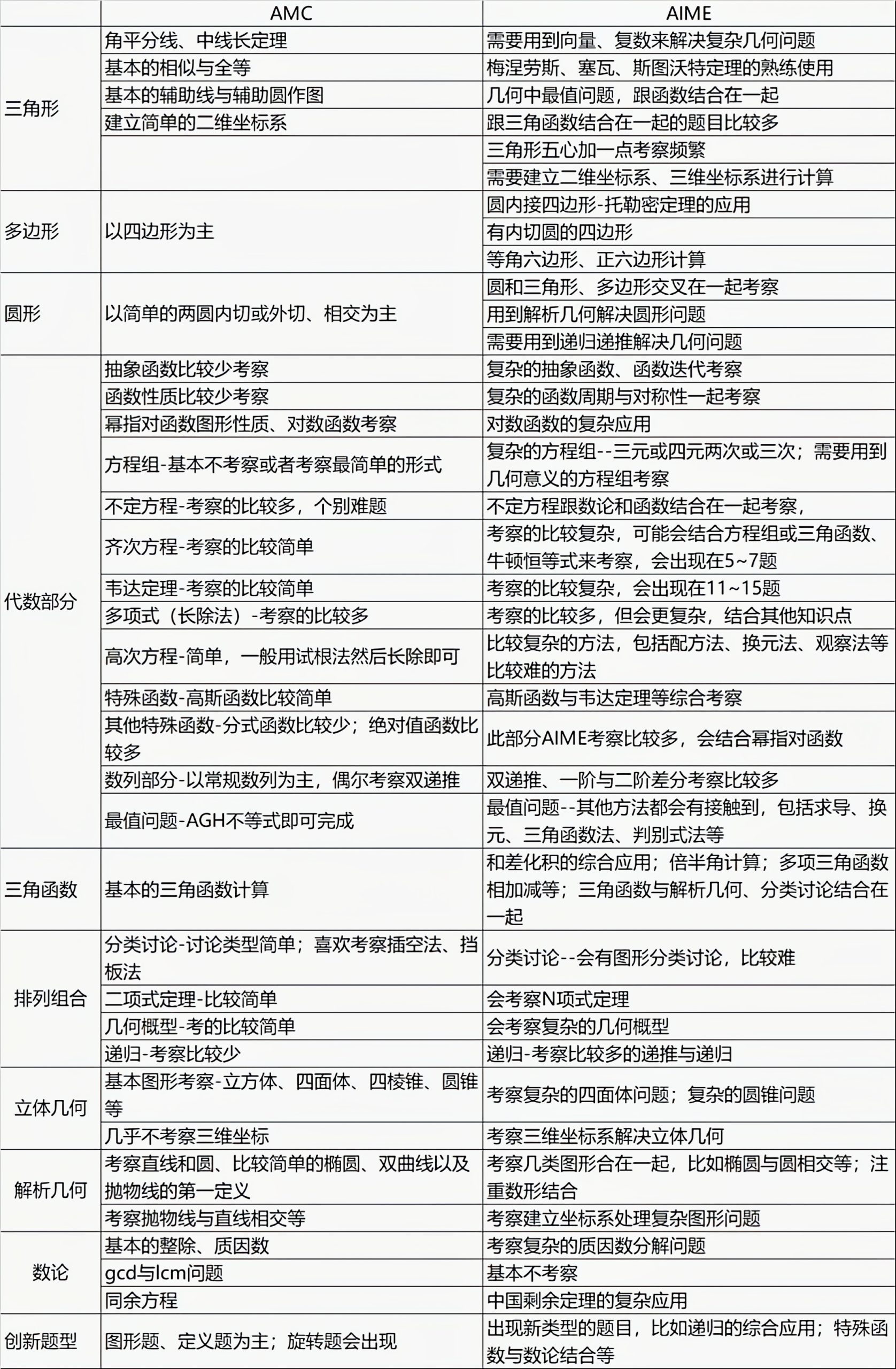
从对比内容可以得出:
AIME(美国数学邀请赛)与AMC(美国数学竞赛)在难度和考察内容上存在显著差异。
①AMC主要考查基础的数学知识和技能,适合于较广泛的学生群体,而AIME则更侧重于学生的综合能力和深度思考。②在处理复数、数论、几何和组合等领域的问题时,AIME要求学生不仅要能理解相关的理论知识,还要能够在复杂的情境中灵活应用这些知识。
此外,AIME强调的是“最优化计算路径”的寻找,学生在解题时需要评估不同的解决方案,选择最有效的计算方式,以减少计算错误和时间浪费。
四、AMC10/12晋级AIME需要补充的知识点
从AMC10晋级AIME需要补充的内容:
对于从AMC10过渡到AIME的学生来说,所需补充的知识点相对较多,因为AMC12与AIME的重叠度更高。因此,参加AMC10的学生在晋级AIME后需要着重补充以下内容:
代数:复数、单位元、三角函数、三角函数恒等式、对数
几何:余弦定理(Law of Cosines)
排列组合:递归(Recursion)、马尔可夫链(Markov Chain)
数论:与AMC10重合度较高,基础扎实的学生可不需额外学习。
从AMC12晋级AIME需要补充的内容:
对于从AMC12过渡到AIME的学生来说,AIME的考点大部分与AMC12一致,但在几何、数论和组合方面还有少量额外的知识点。这些知识点通常较为复杂,并且一般出现在AIME的后5题中,因此掌握它们对于获得高分至关重要。可以重点学习以下AIME特有的知识点:
代数:内容大致相同于AMC12
几何:Bashing方法(如复平面、中心坐标系等解法)、根轴(Radical Axis)
排列组合:侧重于几何图形上的计数
数论:LTE(Lifting The Exponent)定理、不定方程的解法等
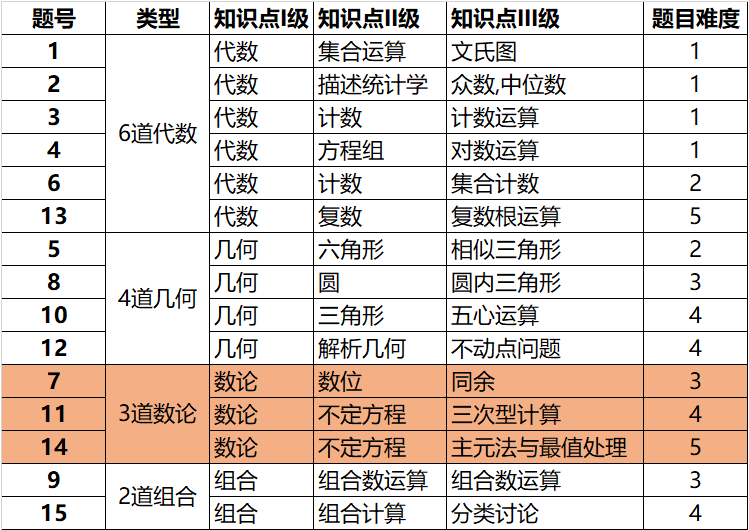
五、近两年 AIME I 试题分析
通过对近两年AIME I卷(American Invitational Mathematics Examination I)的考点进行分析,我们可以将试题大致分为以下两类:
第一类试题:代数与几何为核心。这一类试题的主要特点是以代数和几何为核心,往往需要进行复杂的计算过程。
第二类试题:数论与组合数学为核心。这一类试题主要涉及数论和组合数学,通常要求学生具有较强的逻辑思维能力和熟练的数学技巧。
| 题号 | 2024AIMEI卷考点 | 2023AIMEI卷考点 |
| 1 | 行程问题、方程组求解 | 组合、圆排列 |
| 2 | 对数方程变形、换底对数公式 | 代数、对数的计算 |
| 3 | 必胜策略、找规律 | 组合、算两次 |
| 4 | 条件概率、组合数 | 数论/组合Legendre's Theorem求和技术 |
| 5 | 平面几何、圆幂定理 | 几何、托勒密定理/面积方法 |
| 6 | 图形计数、组合数 | 组合、概率、分步游戏 |
| 7 | 复数、辅助角公式 | 数论/组合、中国剩余定理多个同余方程计数 |
| 8 | 平面几何、内心、相似三角形 | 几何、内切圆的计算 |
| 9 | 双曲线、渐近线 | 代数/组合、多项式的根韦达定理 |
| 10 | 平面几何、弦切角定理 | 数论、利用完系求和 |
| 11 | 图形计数 | 组合、递推、分类 |
| 12 | 函数绘图、三角函数、绝对值函数 |
几何、正弦、余弦定理 |
| 13 | 同余分析、阶 | 几何、平行六面体的体积 |
| 14 | 立体几何、内切球 | 组合、组合计数、等价类 |
| 15 | 函数分析,韦达定理 代数/组合、虚数素数、不等式 | |
六、AIME竞赛难度体现在什么地方?
1、考察内容更深知识面更广
AIME(美国数学邀请赛)不仅考察考生的数学知识广度,还强调对数学知识的深入理解。考生需要熟练掌握多种数学概念和技巧,并能够灵活运用这些知识来解决较为复杂的问题。
从第6题开始,试题的难度逐渐增加。第7题和第8题作为过渡,难度上升,而第9到第15题则进入难题阶段,考生需要具备更高的解决问题能力。
2、几何部分图形更为复杂
在AIME竞赛中,几何部分的难度显著提升。无论是平面几何还是立体几何,解析几何的考察难度已接近中国高考水平。这对考生的空间想象力和几何推理能力提出了更高的要求。