我们的AIME辅导课程配有独家自研教材,授课老师均为海内外名校毕业,具有丰富的竞赛教学经验,个性化定制班课,真正做到有的放矢,事半功倍!可以试听一下~
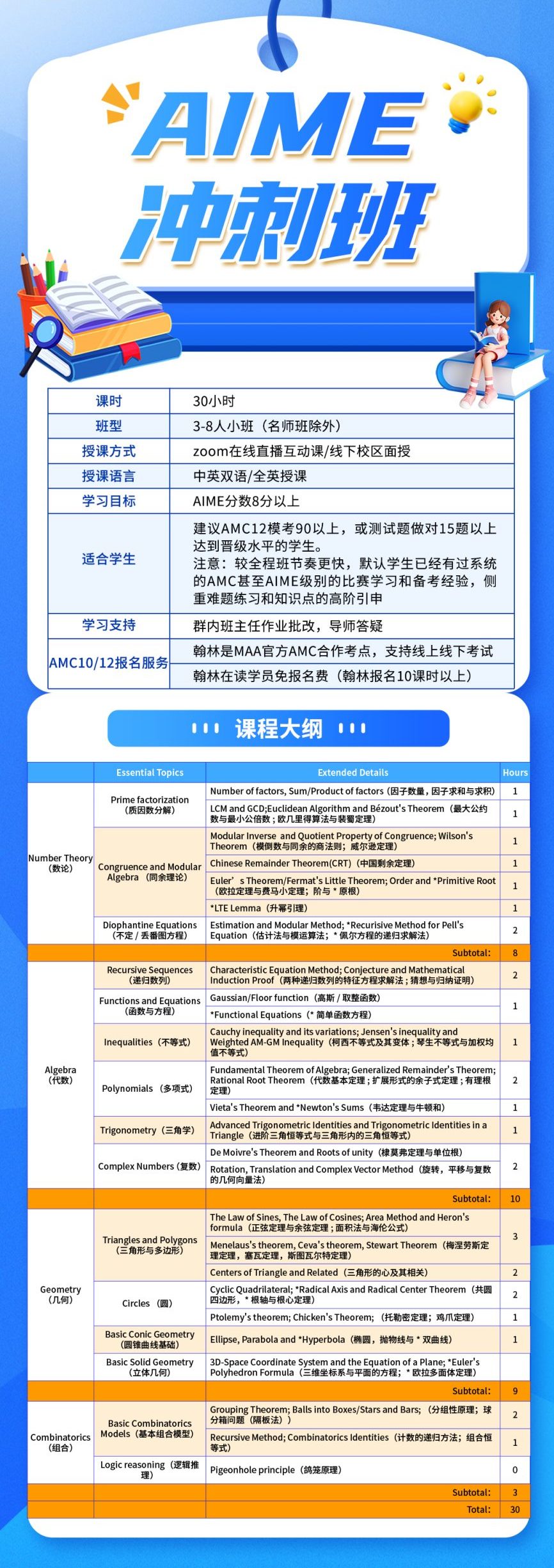
AIME冲刺班
扫码咨询课程详细安排⇓

AIME数学邀请赛核心考点大师课
2H攻克AIME必备核心模块

扫码咨询课程详细安排⇓

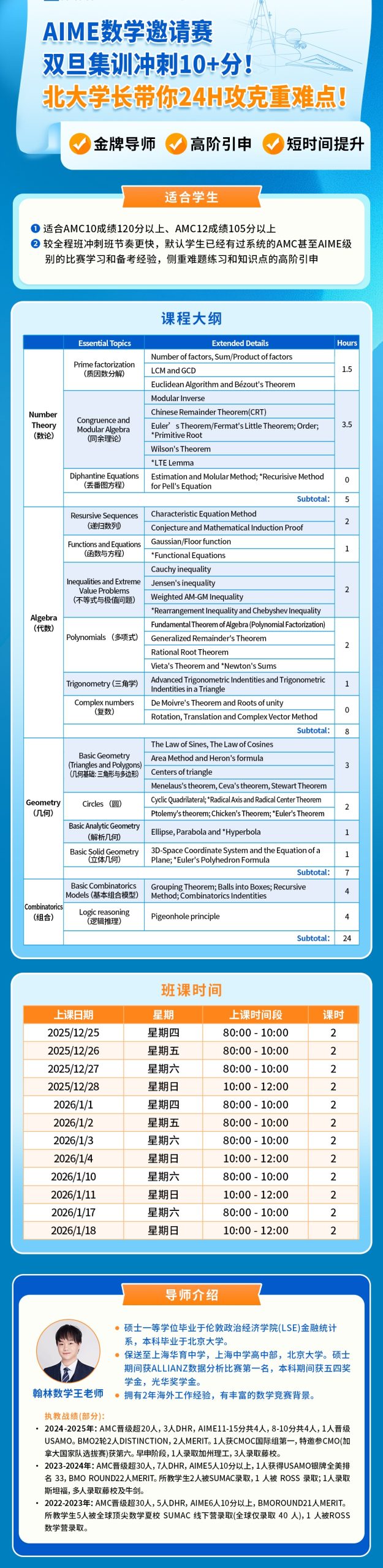
最新课程 AIME数学邀请赛双旦集训冲刺10+分!
北大学长带你24H攻克重难点!
适合学生:
(1)适合AMC10成绩120分以上、AMC12成绩105分以上
(2)较全程班冲刺班节奏更快,默认学生已经有过系统的AMC甚至AIME级
别的比赛学习和备考经验,侧重难题练习和知识点的高阶引申
扫码咨询课程详细安排⇓

AIME课程试听
需要辅导课程的同学,可以扫码咨询,然后选择符合您需求的课程进行试听~

课程示例⇓
AIME数学竞赛全程辅导课程
竞赛介绍
AIME由AMC10和AMC12的优胜者参加,具体晋级比例每年根据参赛人数的比赛结果会有所变化。AIME是介于AMC10、AMC12及美国数学奥林匹克竞赛(USAMO)之间的一个数学竞赛,主要目的是结合AMC10和12的成绩筛选出晋级USAMO的选手,进而通过下一步的比赛与暑期集训(MOP)选拔出6位最终参加IMO(国际数学奥林匹克)的美国国家队成员。竞赛开始于1983年。2000年起AIME增加一场比赛,分为AIMEI和AIMEII两场。
报名须知
1、适合人群:目前水平可以晋级AIME的精英学员
2、AIME培训班为3-8人小班,满3人开班。
注意事项:
学员须知:
受不同学校开学时间影响,班课具体开学时间可能会有微调,具体时间以班课学员为主
班课时间一经确认不再变更,开课后每课若有超半数学员按时出席,则当天正常上课,如有特殊情况请提前告知协调
线上课程:全程互动直播形式,如有需要可以提供课程录播服务
课程大纲
NumberTheory
(1)Primefactorization
①Numberoffactors
②Sum/Productoffactors
③LCMandGCD
④EuclideanAlgorithmandBézout'sTheorem
(2)CongruenceandModularAlgebra
①ChineseRemainderTheorem(CRT)
②Euler’sTheorem/Fermat'sLittleTheorem
③Wilson'sTheorem
(3)DiphantineEquations
①EstimationandMolularMetthod
Algebra
(1)ResursiveSequences
①CharacteristicEquationMethod
②ConjectureandMathematicalInductionProof
(2)FunctionsandEquations
①Gaussian/Floorfunction
②*FunctionalEquations
(3)InequalitiesandExtremeValueProblems
①Cauchyinequality
②Jensen'sinequality
③WeightedAM-GMInequality
④RearrangementInequalityandChebyshevInequality
(4)Polynomials
①FundamentalTheoremofAlgebra(PolynomialFactorization)
②GeneralizedRemainder'sTheorem
③RationalRootTheorem
④Vieta'sTheoremandNewton'sSums
(5)Complexnumbers
①DeMoivre'sTheoremandRootsofunity
②Rotation,TranslationandComplexVectorMethod
Geometry
(1)BasicGeometry(TrianglesandPolygons)
①TheLawofSines,TheLawofCosines
②AreaMethodandHeron'sformula
③Centersoftriangle
④Menelaus'stheorem,Ceva'stheorem,StewartTheorem
(2)Circles
①Inscribedandcircumscribedpolygon/Circle,CyclicQuadrilateral
②Ptolemy'stheorem,*ButterflyTheorem
(3)BasicAnalyticGeometry
①Ellipse,*ParabolaandHyperbola
(4)BasicSolidGeometry
①*Euler'sPolyhedronFormula
Combinatorics
(1)BasicCountingPrinciple SumRulesandProductRules
(2)PermutationsandCombinations
Advancedproblemsincombinatorics
(3)Logicreasoning
Pigeonholeprinciple
扫码免费试听课程⇓

AIME数学竞赛冲刺辅导课程
竞赛介绍
AIME由AMC10和AMC12的优胜者参加,参加标准为:AMC10全球前2.5%或AMC12全球前5%,具体晋级比例每年根据参赛人数的比赛结果会有所变化。AIME是介于AMC10、AMC12及美国数学奥林匹克竞赛(USAMO)之间的一个数学竞赛,主要目的是结合AMC10和12的成绩筛选出晋级USAMO的选手,进而通过下一步的比赛与暑期集训(MOP)选拔出6位最终参加IMO(国际数学奥林匹克)的美国国家队成员。竞赛开始于1983年。2000年起AIME增加一场比赛,分为AIME I和AIME II两场。
注意事项:
1.学员须知:
(1)受不同学校开学时间影响,班课具体开学时间可能会有微调,具体时间以班课学员为主
(2)班课时间一经确认不再变更,开课后每课若有超半数学员按时出席,则当天正常上课,如有特殊情况请提前告知协调
2.线上课程:全程互动直播形式,如有需要可以提供课程录播服务
课程大纲
课程安排:
Number Theory
(1)Prime factorization
① Number of factors
② Sum/Product of factors
③ LCM and GCD
④ Euclidean Algorithm and Bézout's Theorem
(2)Congruence and Modular Algebra
① Chinese Remainder Theorem(CRT)
② Euler’s Theorem/Fermat's Little Theorem
③ Wilson's Theorem
(3)Diphantine Equations
① Estimation and Molular Metthod
Algebra
(1)Resursive Sequences
① Characteristic Equation Method ② Conjecture and Mathematical Induction Proof
(2)Functions and Equations
① Gaussian/Floor function
② *Functional Equations
(3)Inequalities and Extreme Value Problems
① Cauchy inequality
② Jensen's inequality
③ Weighted AM-GM Inequality
④ Rearrangement Inequality and Chebyshev Inequality
(4)Polynomials
① Fundamental Theorem of Algebra (Polynomial Factorization)
② Generalized Remainder's Theorem
③ Rational Root Theorem
④ Vieta's Theorem and Newton's Sums
(5)Complex numbers
① De Moivre's Theorem and Roots of unity ② Rotation, Translation and Complex Vector Method
Geometry
(1)Basic Geometry (Triangles and Polygons)
① The Law of Sines, The Law of Cosines
② Area Method and Heron's formula
③ Centers of triangle
④ Menelaus's theorem, Ceva's theorem, Stewart Theorem
(2)Circles
① Inscribed and circumscribed polygon/Circle, Cyclic Quadrilateral
② Ptolemy's theorem, *Butterfly Theorem
(3)Basic Analytic Geometry
① Ellipse, *Parabola and Hyperbola
(4)Basic Solid Geometry
①*Euler's Polyhedron Formula
Combinatorics
(1)Basic Counting Principle Sum Rules and Product Rules
(2)Permutations and Combinations Advanced problems in combinatorics
(3)Logic reasoning Pigeonhole principle
*(较全程班节奏更快,默认学生已经有过系统的AMC甚至AIME级别的比赛学习和备考经验,侧重难题练习和知识点的高阶引申)
扫码免费试听课程⇓

AIME精编讲义
AIME(American Invitational Mathematics Examination)以其题目难度大、考试时间长而著称,是对学生数学竞赛解题技巧、思维水平和耐力的全面考验。因此,想要在AIME中取得优秀成绩的学生,必须提早准备并制定长期训练规划。

AIME教材由经验丰富的AMC导师编撰整理,分为以下四大版块:
数论:主要包括整除性、同余、质数、数位问题等。数论部分的题目往往需要巧妙的思维和严谨的推理。
代数:涵盖方程与不等式、多项式、函数性质等。代数题目需要学生具备较强的运算能力和逻辑推理能力。
几何:关注平面几何和立体几何,包括圆、三角形、多边形的性质及面积、体积计算等。几何题目考验学生的空间想象力和几何直觉。
组合数学:涉及排列组合、概率、生成函数等。组合题目要求学生具备灵活的思维和创新的解题策略。
高级技巧与奥林匹克知识
教材中适当引入了一些Olympiad级别赛事的知识点和技巧。这些内容帮助学生从更高的维度理解和准备AIME,使他们在面对复杂问题时能够从容应对。
备赛的同学可以扫码咨询AIME竞赛高清版精编讲义⇓


