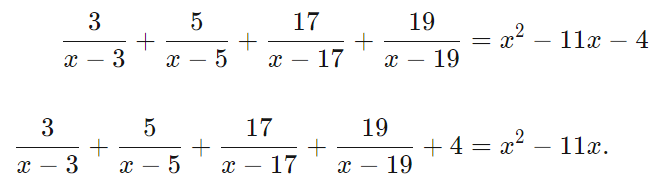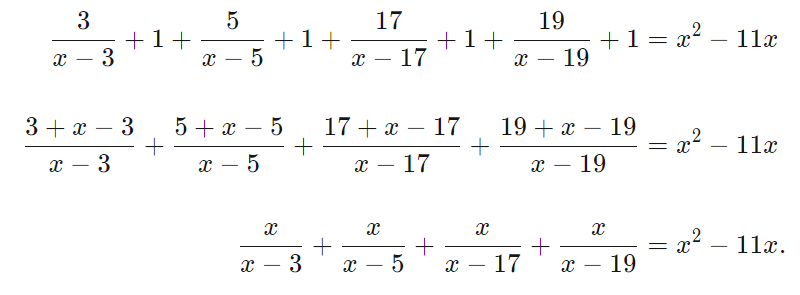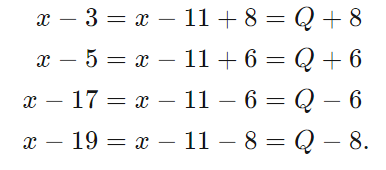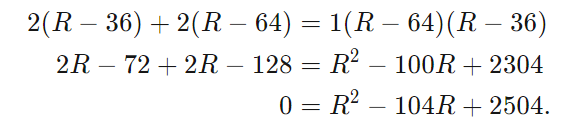AIME困难问题以及详细解法示例

There are many tricks to the AIME that don't show up in a "standard school curriculum." To illustrate, here is an example problem from 2007:

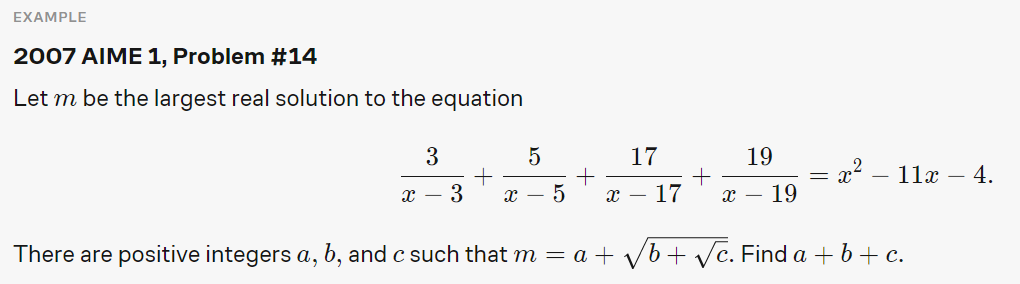
Note that this is in the "hard" set, yet this problem is entirely solvable with regular algebra and even follows the standard logic wanting to isolate $x$ by writing the problem as

$$\text{(some factored polynomial)}=0.$$

However, the specific tricks are unusual; finding them requires practice. This one makes clever use of rearrangement, substitution, and symmetry.

We incidentally can find right away that $x=0$ is a solution:

−1+−1+−1+−1=−4,

so if we find all other solutions are negative, $0$ is our answer. $($However, we are essentially guaranteed in a competition context given the setup of    that there will be a positive root.)

Constants tend to be one of the easiest terms to get rid of; either they can be transformed with substitution (as you'll see later) or they can be "shuffled into" some other part of the algebra. While there's not much possible with the $-4$ on the right-hand side of the equal sign, is there some potential on the left? Let's see:

There are four terms exactly to go with the 4, so what could happen if did rearrangement and split the 4 up to give 1 to each of the terms? We have

​

This is a fairly common competition trick: writing $\text{(some fraction)}+1,$ $\text{(some fraction)}-1,$ or $1-\text{(some fraction)}$ can produce useful results.

Since we're looking for non-zero roots, we can safely divide both sides of the equal sign by $x:$

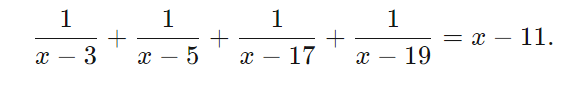
Unfortunately, maneuvering the right side of the equal sign now isn't helpful, so let's look at the terms on the left side instead. There's a definite symmetry pattern going on: −3 and −5 are two apart, and −17 and $-19$ are two apart. The symmetry isn't quite written in a form useful to us, but we can use substitution to help bring it out.

Let $Q=x-11.$ Note that $-11$ is midway between −3 and $-19$ as well as −5 and $-17;$ we picked this number specifically to expose symmetry. It also (by "coincidence") happens to match the right side of the equal sign:

​

Plugging these back into the original equation $($including the right side which has $x-11),$

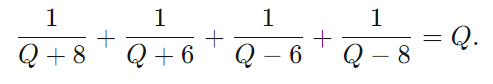
It's tempting to note the matching of +8/-8 and +6/-6. Let's do some more rearrangement and combine the terms:

\[\begin{align} \frac{1}{Q + 8} + \frac{1}{Q - 8} + \frac{1}{Q + 6} + \frac{1}{Q -6} &= Q \\ \frac{Q-8}{(Q + 8)(Q-8)} + \frac{Q+8}{(Q + 8)(Q-8)}+
\frac{Q-6}{(Q + 6)(Q-6)} + \frac{Q+6}{(Q + 6)(Q-6)} &= Q \\ \frac{2Q}{Q^2-64} + \frac{2Q}{Q^2-36} &= Q. \end{align}\]

Not forgetting that $x=11$ is a solution to the original problem, divide by $Q$ on both sides:

We can make the squared terms easier to deal with using another substitution; let's use R=Q²:

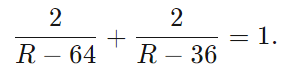
Then get all terms on one side of the equal sign:

​

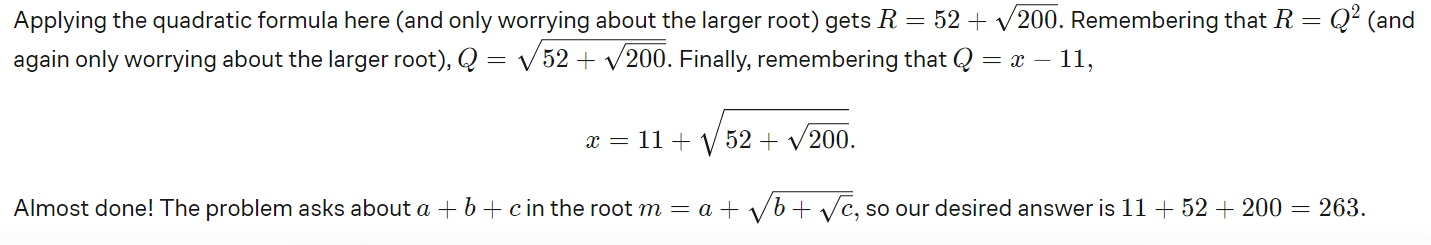
Let's summarize what was used:

• Rearrangement to move the $-4$ term, which caused each of the terms on the left hand of the equal sign to get an $x$ in the numerator.
• Dividing the $x$ out.
• Using a substitution $Q=x-11$ to expose the symmetry that allowed the terms to be more easily combined.
• Using another substitutionR=Q² to avoid dealing with the squared term until necessary.
• Doing standard algebra involving making a quadratic ax²+bx+c=0 and then using the quadratic formula.
• Back-substituting to solve for the largest real solution for $x.$