美国数学邀请赛(AIME)是美国数学协会(MAA)主办的数学竞赛系列中的重要一环,旨在进一步考察高中生的数学能力。AIME是AMC10/12的后续竞赛,通常被视为进入美国数学奥林匹克(USAMO/USAJMO)的敲门砖。AIME以其高难度和严格的考试要求著称,是全球数学竞赛爱好者的一个重要舞台。以下是2025年AIME竞赛的详细安排和相关信息。
一、2025AIME数学竞赛时间
AIME I:2025年2月6日(美东时间)
AIME II:2025年2月12日(美东时间)
AIME I和AIME II是两个独立的考试,提供给学生不同的考试时间选择,以便于安排考试计划和备考时间。然而,学生不能同时报名参加AIME I和AIME II,他们需要根据自己的情况选择其一。
二、AIME竞赛语言与形式
语言:AIME提供中英文双语试卷,方便不同语言背景的学生参加。
形式:竞赛采用线上线下相结合的形式,学生可以选择适合自己的考试方式。
时长:考试时长为3小时,这需要学生具备良好的时间管理能力,以在规定时间内完成所有题目。
评分标准
题型:AIME考试包含15道填空题,每道题的答案为0到999之间的一个整数。
计分:每答对一题得1分,答错或不答不得分,满分为15分。考试没有负分,因此鼓励学生尽可能多地尝试作答。
AIME I 和 AIME II 的选择
选择AIME I或AIME II对于学生来说是一个重要的决定。通过阿思丹报名的学生可以选择参加任意一场,而通过中国区组委会报名的学生只能参加AIME I。根据历年考试情况,AIME I的参与人数较多,而AIME II的分数线通常较低。因此,学生可以根据自己的备考情况和考试策略选择参加哪一场。
三、AIME邀请赛核心考点与备考方法
AIME竞赛核心考点
AIME与AMC10/12的考察范围相似,但在深度和难度上都有所提升。主要考点包括:
代数:涉及方程、不等式、函数等的复杂问题,需要学生具备较强的代数推理能力。
计数:包括排列组合和概率问题,要求学生能够灵活运用组合数学的基本原理。
几何:考察平面几何和立体几何的综合应用,尤其是对几何关系的深入理解。
数论:涉及整除性、同余、质数等问题,要求学生具备扎实的数论基础。
概率:考察随机事件的分析和概率计算能力,需要学生能够从多个角度理解概率问题。
AIME竞赛难度与备考
AIME相较于AMC10/12难度更大,这不仅体现在题型的不同,更在于AIME对知识点的深入挖掘和综合运用的要求。学生需要具备:
熟练掌握多方面的知识点:如代数、几何、数论等,能够灵活运用这些知识解决复杂问题。
计算能力:尤其是在面对大量计算时的坚持和应对策略,这对于在规定时间内完成考试尤为重要。
四、AIME成绩的意义
AIME成绩在申请美国名校和数学夏令营中具有重要的参考价值。以下是AIME成绩在不同申请场景中的竞争力分析:
名校申请:
TOP50院校:AIME成绩达到7分以上在美国TOP50院校中已经具有很强的竞争力。
TOP30院校:申请这些院校通常需要AIME成绩达到8分以上。
TOP20院校:至少需要9分左右的成绩才能在申请中脱颖而出。
数学夏令营申请:如Ross、SUMaC等顶尖夏令营,通常要求AIME成绩达到9分左右,这样的成绩才能在众多申请者中脱颖而出。
AIME竞赛不仅是对学生数学能力的挑战,更是对其思维能力、应试策略和心理素质的综合考验。通过充分的准备和练习,学生能够在AIME竞赛中展现自己的数学才能,为未来的学术发展奠定坚实基础。无论是申请名校还是参与顶尖数学夏令营,AIME的成绩都将成为学生学术能力的重要证明。
我们整理了近十年全部AMC备赛资料,包括AMC8/10/12/AIME的历年真题和答案详解,备赛书籍、知识点地图、备赛公式等,
免费提供给备赛的考试使用,扫码下载即可⇓




![[asy] size(50); 对 A,B; A=(0,0); B=(2,0); 对 C=旋转(60,A)*B; 对 D, E, F; D = (1,0); E=旋转(60,A)*D; F=旋转(60,C)*E; 绘制(C--A--B--循环); 绘制(D--E--F--循环); [/asy]](https://latex.artofproblemsolving.com/1/1/d/11d5abd7384d03c423da478807ee2c6f2a5dfada.png)



![[asy] size(6cm); defaultpen(linewidth(0.7)+fontsize(10)); for(int i=0; i<4; i=i+1) { fill((2*i,0)--(2*i+1,0)--(2*i+1,6)--(2*i,6)--循环,中灰色); } pair A=(1/3,4), B=A+7.5*dir(-17), C=A+7*dir(10); draw(B--A--C); fill((7.3,0)--(7.8,0)--(7.8,6)--(7.3,6)--循环,白色); clip(B--A--C--循环); for(int i=0; i<9; i=i+1) { draw((i,1)--(i,6)); } 标签("$\mathcal{A}$", A+0.2*dir(-17), S);标签("$\mathcal{B}$", A+2.3*dir(-17), S);标签("$\mathcal{C}$", A+4.4*dir(-17), S);标签("$\mathcal{D}$", A+6.5*dir(-17), S); [/asy]](https://latex.artofproblemsolving.com/1/9/8/1985e47141f84873a1d3fffdb0d43fb205c5f8d8.png)
![[asy] // TheMathGuyd 大小(8cm); 对 A=(0,0), B=(4.2,0), C=(5.85,-1.6), D=(4.2,-3.2), EE=(0,-3.2), F=(-1.65,-1.6), G=(0.45,-1.6), H=(3.75,-1.6), I=(2.1,0), J=(2.1,-3.2), K=(2.1,-1.6); 绘制(A--B--C--D--EE--F--循环); 绘制(F--G--(2.1,0)); 绘制(C--H--(2.1,0)); 绘制(G--(2.1,-3.2)); 绘制(H--(2.1,-3.2));标签("$\mathcal{T}$",(2.1,-1.6));标签("$\mathcal{P}$",(0,-1),NE);标签("$\mathcal{Q}$",(4.2,-1),NW);标签("$\mathcal{R}$",(0,-2.2),SE);标签("$\mathcal{S}$",(4.2,-2.2),SW); [/asy]](https://latex.artofproblemsolving.com/6/a/0/6a063c7eb18cc2a02ebddd2f3216e2c02cb09c89.png)
![[asy] unitize(0.50cm); draw((0,-1)--(0,6)); draw((-1,0)--(6,0)); draw(shift(1,1)*unitcircle); draw(shift(1,3)*unitcircle); draw(shift(1,5)*unitcircle); draw(shift(3,1)*unitcircle); draw(shift(3,3)*unitcircle); draw(shift(3,5)*unitcircle); draw(shift(5,1)*unitcircle); draw(shift(5,3)*unitcircle); [/asy]](https://latex.artofproblemsolving.com/4/2/0/420456ae501936e7d4f9073b71122dd6cea147d6.png)








 时求余数。
时求余数。

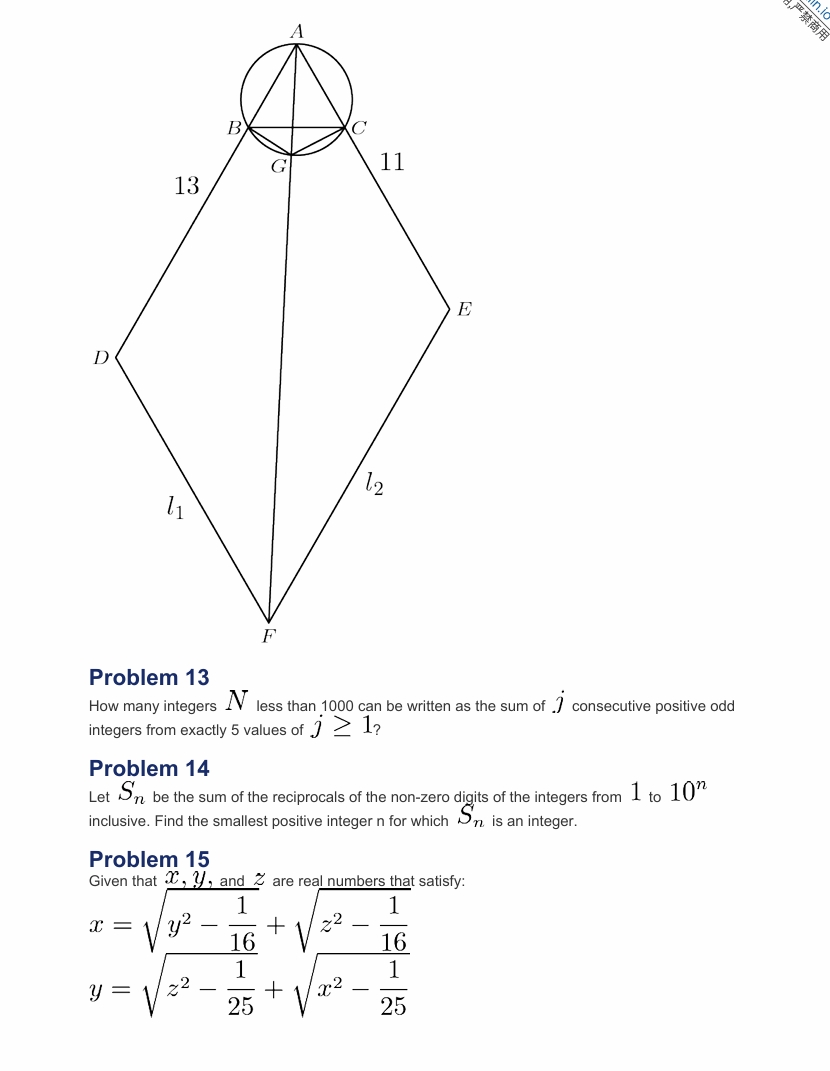
 和
和



![[asy] unitize(0.25inch); defaultpen(linewidth(0.7)); int i,j; for(i = 0; i < 4; ++i) for(j = 0; j < 4; ++j) dot(((real)i, (real)j)); [/asy]](https://latex.artofproblemsolving.com/1/6/e/16ed1460ee16eabb872eb9645928df7b6cf2f60a.png)







![[asy] unitize(3mm); defaultpen(linewidth(.8pt)); dotfactor=4; 对 A=(0,0), D=8*dir(330), C=8*dir(210), B=7*dir(90); 对 Ep=(0,4-27/5); 对[] dotted={A,B,C,D,Ep}; 绘制(圆(A,10)); 绘制(圆(B,3)); 绘制(圆(C,2)); 绘制(圆(D,2)); 绘制(圆(Ep,27/5)); dot(dotted); 标签("$E$",Ep,A); 标签("$A$",A,W); 标签("$B$",B,W); 标签("$C$",C,W); 标签("$D$",D,E); [/asy]](https://latex.artofproblemsolving.com/6/1/7/617cea11001dccad1fa9b6b14c9d0e4236d4d751.png)
 用最简分数表示时,其分母
用最简分数表示时,其分母




