2007年 AIME I 数学邀请赛真题
问题 1
小于 24 的正完全平方数中有多少个![]() 是 24 的倍数?
是 24 的倍数?
问题 2
一条 100 英尺长的移动人行道以每秒 6 英尺的恒定速度移动。Al 踏上人行道的起点并站起来。两秒钟后,Bob 踏上人行道的起点,以每秒 4 英尺的恒定速度沿着人行道向前漫步。两秒钟后,Cy 到达人行道的起点,以每秒 8 英尺的恒定速度沿着人行道快速向前行走。在某个时间,这三个人中的一个正好位于另外两个人的中间。此时,求出人行道起点与中间人之间的距离(以英尺为单位)。
问题 3
复数![]() 等于
等于![]() ,其中
,其中![]() 为正实数且
为正实数且![]() 。假设
。假设![]() 和的虚部
和的虚部![]() 相同,那么
相同,那么![]() 等于什么?
等于什么?
问题4
三颗行星在同一平面上绕恒星旋转。每颗行星都以相同的方向和恒定的速度移动。它们的周期分别为![]() 、
、![]() 和
和![]() 年。这三颗行星和恒星目前共线。从现在起,它们最少需要多少年才能再次共线?
年。这三颗行星和恒星目前共线。从现在起,它们最少需要多少年才能再次共线?
问题5
![]() 将华氏温度转换为相应的摄氏温度的公式
将华氏温度转换为相应的摄氏温度的公式![]() 是
是![]() 将整数华氏温度转换为摄氏度,四舍五入到最接近的整数,再转换回华氏温度,然后再次四舍五入到最接近的整数。
将整数华氏温度转换为摄氏度,四舍五入到最接近的整数,再转换回华氏温度,然后再次四舍五入到最接近的整数。
![]() 对于介于和之间的多少个整数华氏度温度,
对于介于和之间的多少个整数华氏度温度,![]() 原始温度等于最终温度?
原始温度等于最终温度?
问题 6
一只青蛙被放在数轴的原点,并按照以下规则移动:在给定的移动中,青蛙要么前进到最近的具有更大整数坐标且是 的倍数的点,要么前进到最近的具有更大整数坐标且是 的倍数的点。移动序列是与有效移动相对应的坐标序列,以 开头,以 结尾。例如,是一个移动序列。青蛙可能有多少种移动序列? ![]()
![]()
![]()
![]()
![]()
问题 7
让 
![]() 求除以 1000 的余数。 (
求除以 1000 的余数。 (![]() 是小于或等于 的最大整数
是小于或等于 的最大整数![]() ,
,![]() 是大于或等于 的最小整数
是大于或等于 的最小整数![]() 。)
。)
问题 8
多项式是三次多项式。多项式和都是的因数,那么![]() 的最大值是多少?
的最大值是多少? ![]()
![]()
![]()
![]()
问题 9
在直角三角形中,![]() 直角为
直角为![]() ,
,![]() 且
且![]() 。其直角边
。其直角边![]() 和
和![]() 延伸到
延伸到![]() 和 之外
和 之外![]() 。点
。点![]() 和
和![]() 位于三角形外部,分别是两个半径相等的圆的圆心。以 为圆心的圆
位于三角形外部,分别是两个半径相等的圆的圆心。以 为圆心的圆![]() 与斜边和直角边 的延长线相切
与斜边和直角边 的延长线相切![]() ,以 为圆心的圆
,以 为圆心的圆![]() 与斜边和直角边 的延长线相切
与斜边和直角边 的延长线相切![]() ,两个圆互相外切。任一圆的半径长度都可以表示为
,两个圆互相外切。任一圆的半径长度都可以表示为![]() ,其中
,其中![]() 和
和![]() 是互质正整数。求
是互质正整数。求![]() 。
。
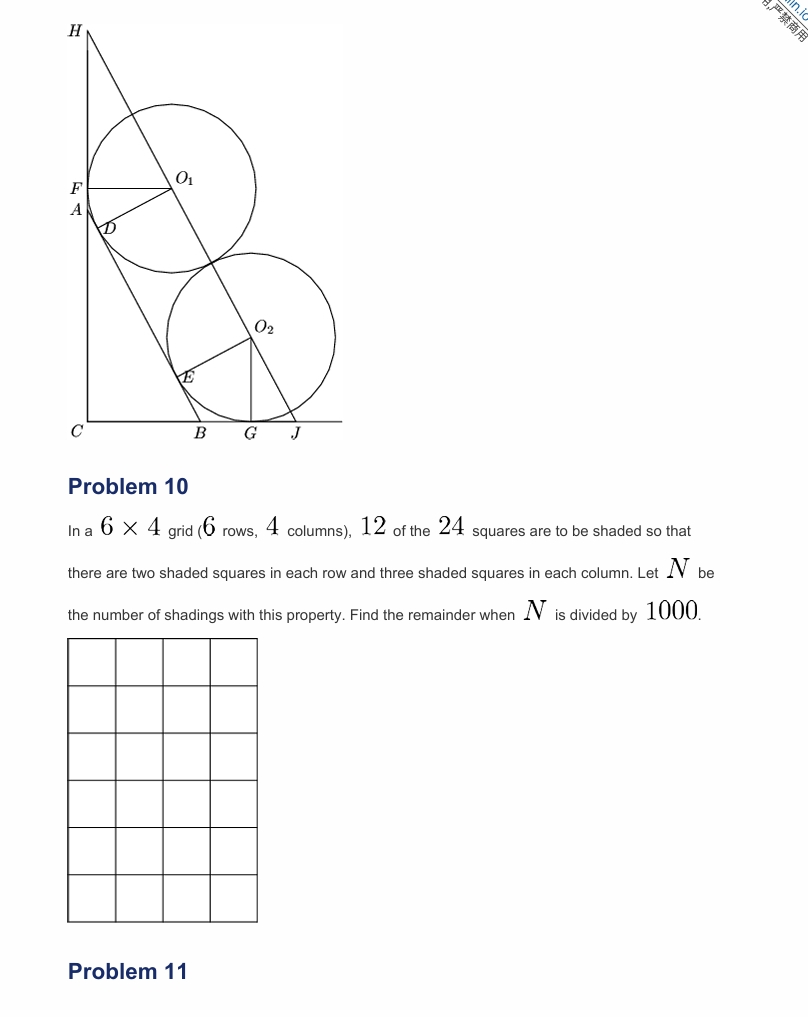
问题 10
在一个![]() 网格(
网格(![]() 行、
行、![]() 列)中,
列)中,![]() 有 的
有 的![]() 方块需要涂黑,使得每行有两个涂黑的方块,每列有三个涂黑的方块。设为具有此属性的涂黑的方块数。求当除以
方块需要涂黑,使得每行有两个涂黑的方块,每列有三个涂黑的方块。设为具有此属性的涂黑的方块数。求当除以![]() 时的余数。
时的余数。 ![]()
![]()
问题11
对于每个正整数![]() ,设
,设![]() 表示唯一正整数,
表示唯一正整数,![]() 使得
使得![]() 。例如,
。例如,![]() 和
和![]() 。如果除以 1000
。如果除以 1000  时求余数。
时求余数。![]()
问题 12
在等腰三角形中![]() ,
,![]() 位于原点,
位于原点,![]() 位于(20,0)。点
位于(20,0)。点![]() 位于第一象限
位于第一象限![]() ,角为
,角为![]() 。如果三角形
。如果三角形![]() 绕点逆时针旋转,
绕点逆时针旋转,![]() 直到的图像
直到的图像![]() 位于正轴上
位于正轴上![]() ,则原始三角形和旋转三角形共同的区域面积为形式
,则原始三角形和旋转三角形共同的区域面积为形式![]() ,其中
,其中![]() 为整数。求
为整数。求![]() 。
。
以下是我们为您整理的全英版pdf真题:

扫码免费获取完整版真题+解析~~~
还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓




