2007年 AIME II 数学邀请赛真题

2007年 AIME II 数学邀请赛真题

问题 1

一个数学组织正在生产一组纪念车牌。每个车牌包含从 AIME 中的四个字母和中的四个数字中选择的五个字符序列 $2007$ 。任何字符在序列中出现的次数都不得超过在 AIME 中的四个字母或中的四个数字中出现的次数 $2007$ 。一组车牌中每个可能的序列都恰好出现一次，包含 N 个车牌。求 N/10。

问题 2

求有序三元组的数量， $(a,b,c)$ 其中 $a$ ，， $b$ 和 $c$ 为正整数， $a$ 是的因数 $b$ ， $a$ 是的因数 $c$ ，且 $a+b+c=100$ 。

问题 3

正方形的 $ABCD$ 边长为 $13$ ，且点 $E$ 和 $F$ 位于正方形的外部，且 $BE=DF=5$ 和 $AE=CF=12$ 。求 $EF^{2}$ 。

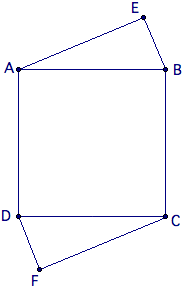
2007 艾梅 II-3.png

问题4

工厂里的工人生产小部件和 whoosits。对于每种产品，所有工人的生产时间都是恒定且相同的，但两种产品的生产时间不一定相等。在一小时内， $100$ 工人可以生产 $300$ 小部件和 $200$ whoosits。在两个小时内， $60$ 工人可以生产 $240$ 小部件和 $300$ whoosits。在三个小时内， $50$ 工人可以生产 $150$ 小部件和 $百万$ whoosits。查找 $百万$ 。

问题5

方程的图形画在方格纸上，每个方格代表每个方向的一个单位。方格纸上有多少个方格的内部完全位于图形下方且完全位于第一象限？ $9x+223y=2007$ $1$ $1$

问题 6

如果一个整数的十进制表示满足，则称其为奇偶单调整数，如果，则为偶数。有多少个四位数的奇偶单调整数？ $a_{1}a_{2}a_{3}\cdots a_{k}$ $a_{i} <a_{i+1}$ $a_{i}$ $a_{i}>a_{i+1}$ $a_{i}$

问题 7

给定一个实数， $x,$ 让 $\lfloor x \rfloor$ 表示小于或等于的最大整数，对于 $x.$ 某个整数，恰好 $k,$ 存在 $70$ 正整数，并且对于所有满足 $n_{1}, n_{2}, \ldots, n_{70}$ $k=\lfloor\sqrt[3]{n_{1}}\rfloor = \lfloor\sqrt[3]{n_{2}}\rfloor = \cdots = \lfloor\sqrt[3]{n_{70}}\rfloor$ $k$ $n_{i}$ $我$ $1 \leq i \leq 70.$

$\frac{n_{i}}{k}$ 找到的最大值 $1\leq 等于 \leq 70.$

问题 8

一张长方形的纸的尺寸为 4 个单位乘以 5 个单位。纸的边缘画有几条平行线。由这些线的交点确定的矩形称为基本矩形，如果

（i）矩形的四条边都是画出的线段，并且

(ii) 所画线段均不位于矩形内。

假设所有画出的线段的总长度恰好为 2007 个单位，设 $N$ 为确定的基本矩形的最大可能数量。求除以 1000 时的余数。 $N$

问题 9

矩形 $ABCD$ 具有和 $AB=63$ 点 $BC=448.$ 和 $E$ 分别 $F$ 位于 $AD$ 和上 $BC$$ ，使得 $AE=CF=84.$ 三角形的内切圆与点相切， $BEF$ 三角形的内切圆与点相切查找 $EF$ $P,$ $DEF$ $EF$ $Q.$ $PQ.$

问题 10

设 $S$ 为有六个元素的集合。设为的所有子集的集合，的子集和不一定不同，是从中独立随机选择的。包含在或中的一个中的概率为其中、和为正整数，为素数，且和互为素数。求（集合是中所有不在中的元素的集合） $\mathcal{P}$ $S.$ $A$ $B$ $S$ $\mathcal{P}$ $B$ $A$ $南非$ $\frac{m}{n^{r}},$ $百万$ $n$ $r$ $n$ $百万$ $n$ $m+n+r.$ $南非$ $S$ $A.$

问题11

两个长度相同但直径不同的长圆柱管平行放置在平面上。较大的管子的半径为，沿平面向半径为的小管子滚动。它在小管子上滚动，并继续沿平面滚动，直到它停止在圆周上的同一点上，此时已完成一整圈。如果小管子不动，滚动时没有滑动，则大管子最终会与起始位置相距一段距离。该距离可以表示为其中和为整数，不能被任何素数的平方整除。求 $72$ $24$ $x$ $x$ $a\pi+b\sqrt{c},$ $一个，$ $b,$ $c$ $c$ $a+b+c.$