2006年 AIME II 数学邀请赛真题
问题 1
在凸六边形中![]() ,六条边全等,
,六条边全等,![]() 且
且![]() 为直角,且
为直角,且![]() 和
和![]() 全等。六边形区域的面积
全等。六边形区域的面积![]() 为
为![]() 。
。
问题 2
面积为正的三角形的边长分别为![]() 、
、![]() 和
和![]() ,其中
,其中![]() 为正整数。求 的可能值的数量
为正整数。求 的可能值的数量![]() 。
。
问题 3
设![]() 为前 100 个正奇数的乘积。找出能被 整除的
为前 100 个正奇数的乘积。找出能被 整除的![]() 最大整数。
最大整数。 ![]()
![]()
问题4
设是的 ![]() 排列,
排列,![]()
![]()
这种排列的一个例子是![]() 查找此类排列的数量。
查找此类排列的数量。
问题5
掷一个六面骰子,骰面数为![]() ,且
,且![]() ,掷出正面的概率
,掷出正面的概率![]() 大于
大于![]() ,掷出反面的概率小于
,掷出反面的概率小于![]() ,掷出其他四个面中的任意一个的概率为
,掷出其他四个面中的任意一个的概率为![]() ,反面数字之和为 7。掷两个这样的骰子,掷出和为 7 的概率为
,反面数字之和为 7。掷两个这样的骰子,掷出和为 7 的概率为![]() 。已知掷出正面的概率
。已知掷出正面的概率![]() 为
为![]() 其中
其中![]() 和
和![]() 为互质正整数,求
为互质正整数,求![]()
问题 6
正方形![]() 的边长为 1。点
的边长为 1。点![]() 和分别
和分别![]() 位于
位于![]() 和上
和上![]() ,所以
,所以![]() 是等边的。一个正方形的顶点为,
是等边的。一个正方形的顶点为,![]() 其边与的边平行
其边与的边平行![]() ,顶点位于
,顶点位于![]() 这个小正方形的边长为,
这个小正方形的边长为,![]() 其中
其中![]() 和
和![]() 为正整数,
为正整数,![]() 不能被任何素数的平方整除。求
不能被任何素数的平方整除。求![]()
问题 7
找出有序正整数对的数量,![]() 使得
使得![]() 和都
和都![]() 没有
没有![]() 零位。
零位。
问题 8
用彩色纸做成的全等等边三角形数量无限。每个三角形都是纯色,纸张的两面颜色相同。用四个这样的纸三角形可以构成一个大等边三角形。如果无法通过平移、旋转和/或反射将一个大三角形放在另一个大三角形上,使得它们对应的小三角形颜色相同,则认为两个大三角形是可区分的。
假设有六种不同颜色的三角形可供选择,可以形成多少个可区分的大等边三角形?![[asy] size(50); 对 A,B; A=(0,0); B=(2,0); 对 C=旋转(60,A)*B; 对 D, E, F; D = (1,0); E=旋转(60,A)*D; F=旋转(60,C)*E; 绘制(C--A--B--循环); 绘制(D--E--F--循环); [/asy]](https://latex.artofproblemsolving.com/1/1/d/11d5abd7384d03c423da478807ee2c6f2a5dfada.png)
问题 9
圆![]() 和
和![]() 圆心分别位于 (0,0)、(12,0) 和 (24,0),半径分别为 1、2 和 4。线是和的
圆心分别位于 (0,0)、(12,0) 和 (24,0),半径分别为 1、2 和 4。线是和的![]() 共同内切线,斜率为正,线是和的共同内切线,斜率为负。假设线和相交于和,其中和为正整数,不能被任何素数的平方整除,求
共同内切线,斜率为正,线是和的共同内切线,斜率为负。假设线和相交于和,其中和为正整数,不能被任何素数的平方整除,求![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
问题 10
七支球队参加一场足球锦标赛,每支球队与其他球队只交手一次。没有平局,每支球队都有机会![]() 赢得每场比赛,比赛结果是独立的。在每场比赛中,获胜者获得一分,失败者获得 0 分。总分累计以决定球队的排名。在锦标赛的第一场比赛中,球队
赢得每场比赛,比赛结果是独立的。在每场比赛中,获胜者获得一分,失败者获得 0 分。总分累计以决定球队的排名。在锦标赛的第一场比赛中,球队![]() 击败球队,球队得分高于球队的
击败球队,球队得分高于球队的![]() 概率为,其中和是互质正整数。求
概率为,其中和是互质正整数。求![]()
![]()
![]()
![]()
![]()
![]()
问题11
序列定义如下![]() ,对于所有正整数,
,对于所有正整数,![]() 假设
假设![]() 和求除以 1000 的
和求除以 1000 的 ![]() 余数。
余数。![]()
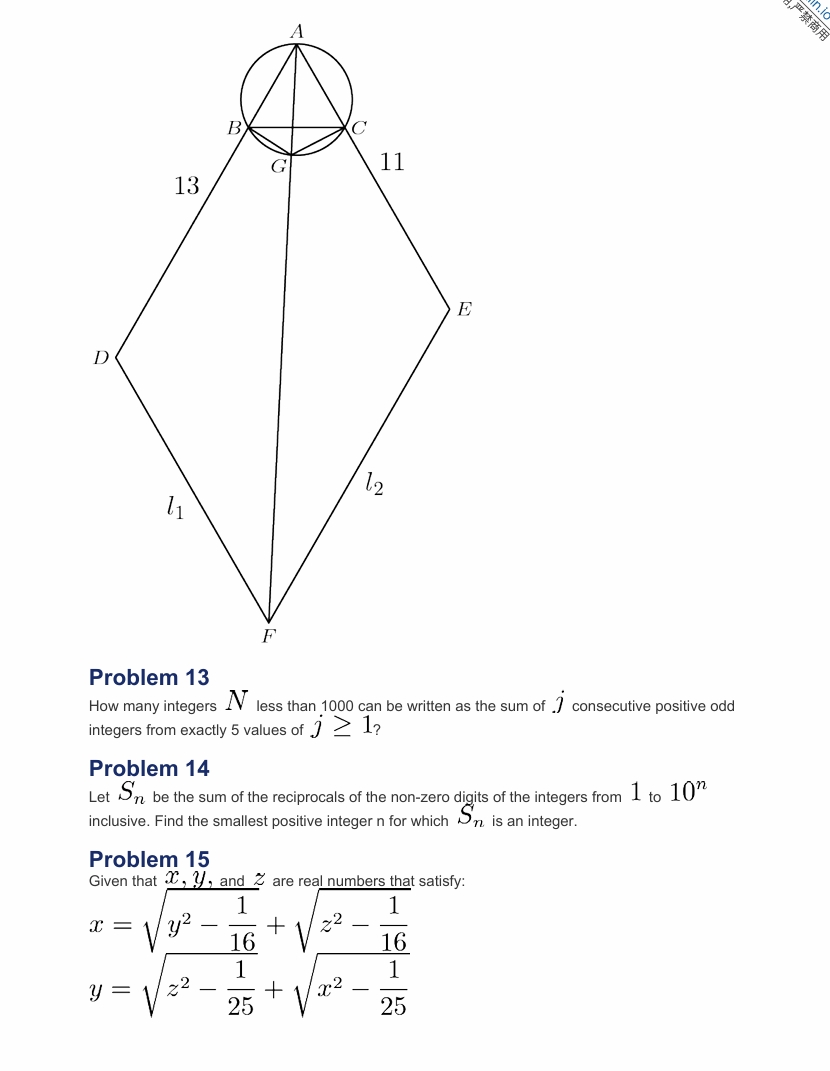
问题 12
等边内![]() 接于半径为 2 的圆。延伸
接于半径为 2 的圆。延伸![]() 到点
到点![]() ,
,![]() 使得
使得![]() 和延伸
和延伸![]() 到点
到点![]() ,
,![]() 使得
使得![]() 通过
通过![]() 画一条
画一条![]() 与和平行的线
与和平行的线![]() 和通过画一条与平行的
和通过画一条与平行的![]() 线让和为交点让和为圆上与和共线且不同于的点鉴于的面积可以表示为形式 其中和为正整数,和 为互质,并且不能被任何素数的平方整除,求
线让和为交点让和为圆上与和共线且不同于的点鉴于的面积可以表示为形式 其中和为正整数,和 为互质,并且不能被任何素数的平方整除,求![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
以下是我们为您整理的全英版pdf真题:

扫码免费获取完整版真题+解析~~~
我们整理了近十年全部AMC备赛资料,包括AMC8/10/12/AIME的历年真题和答案详解,备赛书籍、知识点地图、备赛公式等,
免费提供给备赛的考试使用,扫码下载即可⇓