2025年AIME II中英文真题









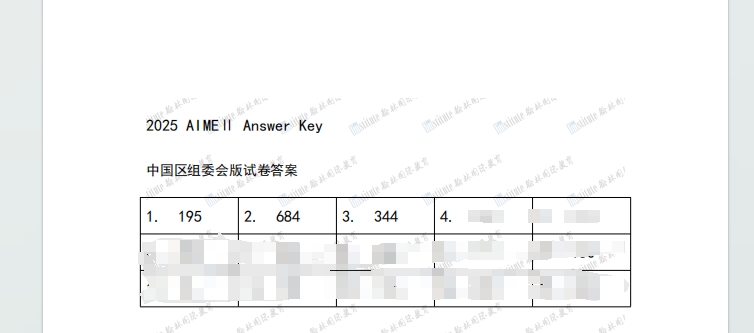
2025年AIME II中英文答案
扫码免费获取完整版真题+解析~~~
还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓



2025年AIME II中英文真题









2025年AIME II中英文答案

扫码免费获取完整版真题+解析~~~
还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓



AIME(美国数学邀请赛)是全球顶尖的数学竞赛之一,对学生数学能力的验证有重要意义,并且在申请美国顶尖大学时也起着加分作用。2025年AIMEⅡ考试已经结束。为了确保比赛的公平性,我们将在官方解禁后(2025年2月14日23:59分后)提供AIMEⅡ的真题、答案及视频解析。
2025 AIME Ⅱ 真题+答案+视频解析
 扫码免费领取⇓
扫码免费领取⇓

AIME考后安排
考试结束后4-6周(具体以官方通知为准):
AIME Ⅱ 成绩将会进行公布
查询方法
中国AMC竞赛组委会
进入www.math-table.com,点击“Scores”输入报名手机号、验证后即可查询成绩。
阿思丹小程序
查询方法:登录“阿思丹国际理科测评”小程序,点击“我的报名”-点击“AIME”-点击“分数查询”,进行成绩查询。
USA(J)MO历年分数线
| 2024年 | ||||
| USAJMO cutoff scores | USAMO cutoff scores | |||
| AMC 10A | AMC 10B | AMC 12A | AMC 12B | |
| AIME Ⅰ | 236 | 232 | 245 | 248 |
| AIME Ⅱ | 230 | 220 | 220 | 228 |
| 2023年 | ||||
| USAJMO cutoff scores | USAMO cutoff scores | |||
| AMC 10A | AMC 10B | AMC 12A | AMC 12B | |
| AIME Ⅰ | 194 | 190.5 | 223 | 227 |
| AIME Ⅱ | 188 | 180 | 214.5 | 226 |
| 2022年 | ||||
| USAJMO cutoff scores | USAMO cutoff scores | |||
| AMC 10A | AMC 10B | AMC 12A | AMC 12B | |
| AIME Ⅰ | 203.5 | 190.5 | 222 | 227.5 |
| AIME Ⅱ | 196.5 | 182 | 208.5 | 203 |
AIME考多少分才有用?
1 基础分数线:7分的“门槛”
满分与平均分:
满分:AIME满分为15分。
平均分:每年的平均分大约在5分左右。
竞争力分数:
7分以上:考到7分以上才被认为是有竞争力的分数。对于申请美国Top 30院校的学生,7分是一个重要的“门槛”。
具体要求:
Top 30院校:7分是一个关键的分数线,表明学生具备较强的数学能力和潜力。
Top 20院校:需要8分以上的成绩才能更具竞争力,显示出更高的学术水平和解题能力。
2 高分段的意义
冲击藤校和G5名校的关键分数:
10分以上:这是冲击藤校(如哈佛、耶鲁、普林斯顿等)和G5名校(如牛津、剑桥等)的关键分数。10分以上的学生不仅在申请中更具竞争力,还有机会晋级USAMO(美国数学奥林匹克竞赛)。
具体意义:
申请优势:10分以上的成绩可以显著提升申请者的竞争力,特别是在竞争激烈的顶尖学府中。
晋级机会:高分者有机会晋级USAMO,进一步展示自己的数学才能。
AIME的“高分段”:
12分以上:通常被认为是AIME的“高分段”,这些学生在全球范围内表现卓越,是数学领域的佼佼者。
具体意义:
全球范围内的认可:12分以上的成绩意味着在全球范围内处于顶尖水平,能够获得更多的学术机会和认可。
顶尖奖项:高分者有机会获得AIME的顶级奖项,进一步提升个人简历的含金量。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓



美国数学邀请赛II(AIME II)是全球范围内的顶级数学竞赛之一。以下是2025年AIME II的详细信息及其考试内容,旨在帮助考生更好地准备和理解考试。
一、AIME II竞赛报考信息
1. 参赛时间与报名截止
参赛时间:2025年2月13日,13:00-16:00(AIME I已取消)
报名截止时间:2025年2月9日
2. 参与方式
只有在AMC10/12中达到晋级线的考生才能获得组委会的邀请参加AIME II。
3. 考试时长与语言
考试时长:3小时
考试语言:待定(可能为双语或仅限英语)
4. 考试费用与形式
考试费用:晋级考生无需缴纳任何报名费或考务费。
考试形式:线上进行,15道填空题,每道题答案在000-999之间。
5. 评分标准
满分:15分
计分:每题答对得1分,答错不扣分
二、AIME竞赛分数的意义
1. 6-7分
虽然不能直接晋级USAMO,但这个分数段仍能证明考生在基础数学知识上的扎实能力。如果目标是申请非数学类名校,这一成绩可为申请增添亮点。
2. 8-10分
这是一个相对较强的成绩,通常能让考生进入数学能力较强的学校的数学课程,并有机会通过USAMO的选拔。对希望进入名校数学或理工科专业的考生来说,这个分数具有明显的加分效果。
3. 11-12分
成绩非常优秀,通常能直接进入USAMO选拔阶段。对顶尖名校的数学系或其他理工科专业申请者来说,这是一个极具竞争力的成绩。
4. 13-15分
AIME的顶级成绩,证明考生在数学领域的超强能力。这个分数几乎可以确保获得USAMO资格,并在名校申请中极具竞争力。
三、AIME竞赛考试内容
1. 代数
多项式:根与系数的关系、因式分解、多项式除法等。
方程与函数:对数函数、三角函数、二元二次方程等。
数列:递推关系、等差与等比数列的性质及求和。
不等式:均值不等式、柯西不等式、排序不等式。
对数、复数与三角函数:基本运算及几何应用。
2. 几何
平面几何:三角形多心问题、塞瓦定理、正余弦定理、Stewart定理。
立体几何:体积计算、内切球与外接球问题。
解析几何:二维与三维坐标系应用,圆锥曲线知识。
3. 数论
同余理论:高次同余方程、指数型同余计算。
整除性质:整除判定、最大公因数与最小公倍数。
4. 组合数学
排列组合:二项式定理、组合恒等式、映射方法、容斥原理。
概率:古典概型、几何概型、条件概率、Bayes公式、概率期望。
AIME II不仅考察学生的数学基础和解题技巧,还要求考生具备灵活的思维能力和综合分析问题的能力。通过准备和参与AIME II,考生可以在数学竞赛中提升自己的能力,并为未来的学术和职业发展打下坚实基础。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓




2025年AIME II(American Invitational Mathematics Examination II)即将开考,以下是关于考试的详细安排和备考建议。

一、2025赛季AIME考试安排
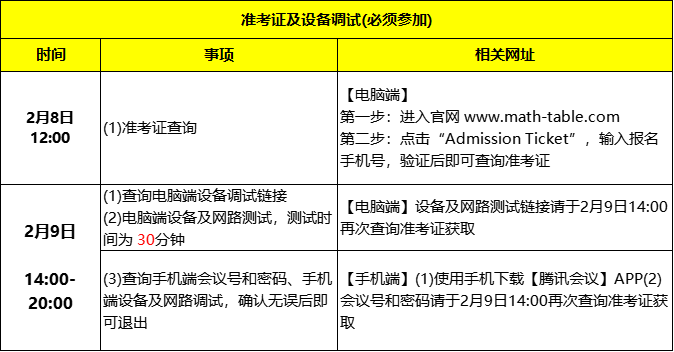
1. 准考证查询
查询时间:2025年2月8日12点起
查询方式:
进入官网 www.math-table.com
点击“Admission Ticket”,输入报名手机号,验证后即可查询准考证
2. 考试时间与形式
考试时间:2025年2月13日 13:00-16:00
考试形式:线上考试
考试语言:待定(具体情况等待官方通知)
考试时长:3小时
竞赛形式:15道填空题,每道题答案的区间为000-999
评分标准:满分15分,答对1题得1分,答错不扣分
二、AIME竞赛难度分析
1. 题目分类
AIME的题目主要分为两类:
代数与几何结合类:以代数和几何为核心,穿插复杂的计算,有时需要运用数论或数值分析方法。
纯粹的数论与组合类:涉及组合数计算、各种公式和数论分析技巧。
2. 难度分布
1-6题:难度较低,相当于AMC12的前20题或AMC10的前23题,主要考查基础知识和基本解题方法。
7-10题:难度逐渐增加,涉及复杂的不定方程、复数、高斯函数等问题,需要综合分析能力和解题技巧。
11-15题:难度最高,涉及复杂的数论和组合问题,如高次方程的整数解、复杂的组合计数等,需要深入思考和创新解题方法。
三、考试基本信息
1. 考试时间管理
提前查询考试日期和时间,确保准确掌握时间,提前30分钟到达考场或准备好线上考试环境,应对突发情况。
确保设备和网络正常运行,避免考试中出现卡顿或掉线。
2. 携带物品
证件:携带有效身份证明文件,如护照、身份证等。
文具:准备充足的书写工具,如黑色中性笔、铅笔、橡皮、直尺等。
计算器:了解考试允许使用的计算器型号,确保计算器电量充足,并熟悉其操作功能。
3. 准备工作
下载准考证:提前下载并熟悉准考证。
熟悉考试平台:提前熟悉腾讯会议和考试系统,确保考试当天能够顺利登录并使用。
调试设备:确保网络连接稳定,设备运行正常,避免因技术问题影响考试。
四、答题规范与技巧
1. 答题时间分配
平均每道题有8分钟的作答时间,合理分配时间,优先完成得分较高的题目。
遇到难题时,不要过度纠结,先跳过,确保会的题目不失分。
2. 答题格式
按照答题卡上的说明填写答案,结果的表达形式必须符合题目要求,否则即使答案正确也可能因为格式错误而不能得分。
AIME的答案必须是000-999之间的整数,无需解答步骤,只需写出答案即可。
五、知识与技能储备
1. 复习知识点
全面回顾:对代数、几何、函数、概率等各个知识板块进行全面复习,梳理重要的公式、定理和解题方法。
强化重点:针对AIME竞赛中常考的重点内容,如数列、数论、组合数学等,进行有针对性的强化复习。
2. 回顾错题
整理错题集:将平时练习和模拟考试中的错题进行整理,分析错误原因。
分类总结:按照知识点和错误类型对错题进行分类,总结解题技巧和易错点。
3. 模拟考试
限时训练:按照考试时间和要求,进行全真模拟考试,提高解题速度和准确率。
适应节奏:通过多次模拟考试,适应AIME竞赛的考试节奏和难度,找到适合自己的答题顺序和策略。
六、心理与身体状态
1. 心理调适
保持积极心态:相信自己的能力,以平和、稳定的心态对待考试。
调整期望:明确AIME竞赛的难度较高,将考试视为提升能力的机会,无论成绩如何,都能从中收获经验和成长。
2. 身体状态
合理作息:保持规律的作息时间,保证充足的睡眠,避免熬夜和过度疲劳。
饮食健康:注意饮食卫生和营养均衡,避免食用过于油腻、辛辣或刺激性的食物,考前适当补充富含蛋白质、维生素和矿物质的食物。
七、特殊情况处理
1. 线上考试注意事项
草稿纸画图:尤其是几何题中,无论是否提供图形,都建议重新画图以便更好地理解和解答。
双语试卷:如果试卷是双语的,先阅读自己熟悉的语言,如果对题目有疑问,再参考另一种语言来确认。
通过以上信息和建议,考生可以更好地准备2025 AIME II竞赛,争取在考试中取得优异成绩。祝所有考生好运!
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓




美国数学邀请赛(American Invitational Mathematics Examination,简称AIME)是美国数学竞赛体系中的一项重要赛事。它为在数学方面表现优异的学生提供了一个展示自我能力的平台,同时也为选拔和培养具有数学天赋的学生提供了机会。AIME不仅是美国国家队选拔的关键一步,还为国际数学奥林匹克(IMO)和欧洲女子数学奥林匹克(EGMO)培养人才。
一、AIME的参赛资格
AIME的参赛资格基于学生在美国数学竞赛10(AMC10)或美国数学竞赛12(AMC12)中的表现。每年,AMC10成绩排名前约2.5%的学生和AMC12成绩排名前约5%的学生有资格参加AIME。具体的分数线会根据当年的考试整体情况进行调整。通过MOP(Mathematical Olympiad Program)的测试,一组精选的学生被邀请参加团队选拔测试(TST),以确定代表美国参加国际赛事的团队。
二、AIME考试内容
AIME的考试内容与AMC10/12相似,但难度更大,要求考生具备扎实的数学基础和灵活的数学思维。考试内容包括:
1. 代数
涵盖函数、方程、数列、不等式等内容。
2. 几何
包括平面几何、立体几何和解析几何。
3. 数论
涉及整数的性质、同余、因数与倍数、质数与合数等。
4. 组合
包含排列组合、概率、计数原理等。
AIME强调学生的综合能力和深度思考。在处理复数、数论、几何和组合等领域的问题时,学生不仅需要理解相关的理论知识,还要能够在复杂情境中灵活应用这些知识。此外,AIME注重“最优化计算路径”的寻找,要求学生在解题时评估不同的解决方案,选择最有效的计算方式,以减少计算错误和时间浪费。
三、AIME赛事规则
AIME考试由15道简答题组成,考试时间为3小时。考试语言为英语,要求学生具备一定的英语数学词汇量和阅读理解能力,以准确理解题目要求。AIME通常在每年2月份举行,分为AIME Ⅰ和AIME Ⅱ两场比赛。晋级的学生可以选择参加AIME Ⅰ或AIME Ⅱ,但不能同时参加。
四、如何从AMC晋级AIME?
1. 从AMC10晋级AIME
对于从AMC10过渡到AIME的学生来说,需要补充的知识点相对较多。特别是在代数和组合方面,学生需要掌握复数、单位元、三角函数、三角函数恒等式、对数、递归(Recursion)和马尔可夫链(Markov Chain)等内容。
2. 从AMC12晋级AIME
AMC12与AIME的考点大部分一致,但在几何、数论和组合方面有少量额外的知识点。学生需掌握Bashing方法、根轴(Radical Axis)、几何图形上的计数、LTE定理和不定方程的解法等。
五、AIME的意义
AIME不仅是展示学生数学能力的平台,也是培养数学精英的重要步骤。通过参加AIME,学生能够深化对数学的理解,提升解题能力和思维能力。这不仅对他们的学术发展有帮助,也为他们在国际数学竞赛中的表现奠定了基础。
总之,AIME是美国数学竞赛体系中不可或缺的一环,通过层层选拔,为美国乃至全球的数学精英提供了展示和提升自我的机会。参加AIME不仅是对学生数学能力的挑战,也是他们迈向更高数学殿堂的一次重要历练。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓




美国数学邀请赛(AIME)是一个面向全球优秀高中生的数学竞赛,具有较高的挑战性和权威性。以下是AIME考试的详细信息和备考建议,旨在帮助考生更好地理解考试结构和提高备考效率。
一、AIME考试基本信息
1. 考试时长与语言
考试时长:3小时
试卷语言:中英双语
2. 试卷构成
题型:15道填空题
答案范围:每道题的答案都是000-999之间的整数
3. 计分方式
满分:15分
计分:每题答对得1分,答错不扣分
二、AIME与AMC10/12的差异
1. 考试形式的差异
AIME从AMC10/12的选择题形式转变为填空题形式,考试时间延长到3小时。这意味着考生需要深入理解题意,通过推理和计算解决问题,而不能依赖选择题的技巧,如排除法等。这种形式考验考生的数学基本功和计算稳定性。
2. 知识点的扩展
AIME的考点与AMC12大致相同,但在几何、数论、组合模块中增加了一些复杂知识点,通常出现在AIME的后5题。掌握这些知识点对于取得高分至关重要。备考AIME的考生应先了解AMC12相比AMC10新增的内容。
AIME新增核心知识点:
几何:三角形的多心问题、根轴与根心、塞瓦定理、位似变换
数论:高次同余方程、指数型同余、线性不定方程
组合:无穷时间状态的期望问题、生成函数、图论
AMC12新增核心知识点:考试准备与策略
代数:对数、三角函数、复数、单位根、多项式根、圆锥曲线、三维坐标系
几何:圆幂、圆内接多边形、正余弦定理、Stewart定理
数论:中国剩余定理
组合:递推计数、插板法
3. 题目的灵活性和综合性
AIME题目以其灵活性和综合性著称,需要考生具备发散性思维,理解和联想题目背后的数学思想。题目可能涉及多模块知识点,考生需灵活运用各种数学技巧来解决问题。
三、考试准备与策略
1. 确定目标和答题策略
确定自己的目标分数(如8分、10分、12分等),制定相应的答题策略。
合理分配时间,控制每道题目的解题时间,留出时间检查。
2. 根据强弱调整答题顺序
均衡型:水平均衡的考生可以按顺序答题,遇到困难题目及时跳过。
模块回避型:在薄弱模块上跳过题目,优先完成其他题目。
模块优先型:根据强弱顺序解题,从强项开始。
3. 记住关键定理和公式
考生需记住代数、几何、数论、组合等领域的重要定理和公式,以便在考试中灵活应用。
4. 解题技巧与方法
考虑几何题是否可以建系解决,计算量是否合适。
递推数列问题应先找规律,考虑累加、累乘或特征方程。
组合题中“至少存在”类问题考虑用补数法或容斥原理。
5. 考场注意事项
仔细读题,标记重要信息;线上考试时在草稿纸上记录重点。
几何题在草稿纸上画图,使用不同颜色的笔。
组织草稿,方便检查计算结果。
通过系统的备考和合理的考试策略,考生可以在AIME中充分展现自己的数学能力,取得优异成绩。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓




美国数学邀请赛(AIME)是国际数学竞赛中极具影响力的赛事之一,难度高于AMC10和AMC12。AIME的成绩在大学申请中扮演着重要角色,优秀的成绩不仅为学生增添光彩,还可能晋级至美国数学奥林匹克竞赛(USAMO)。

一、2025AIME竞赛最新变动!!!
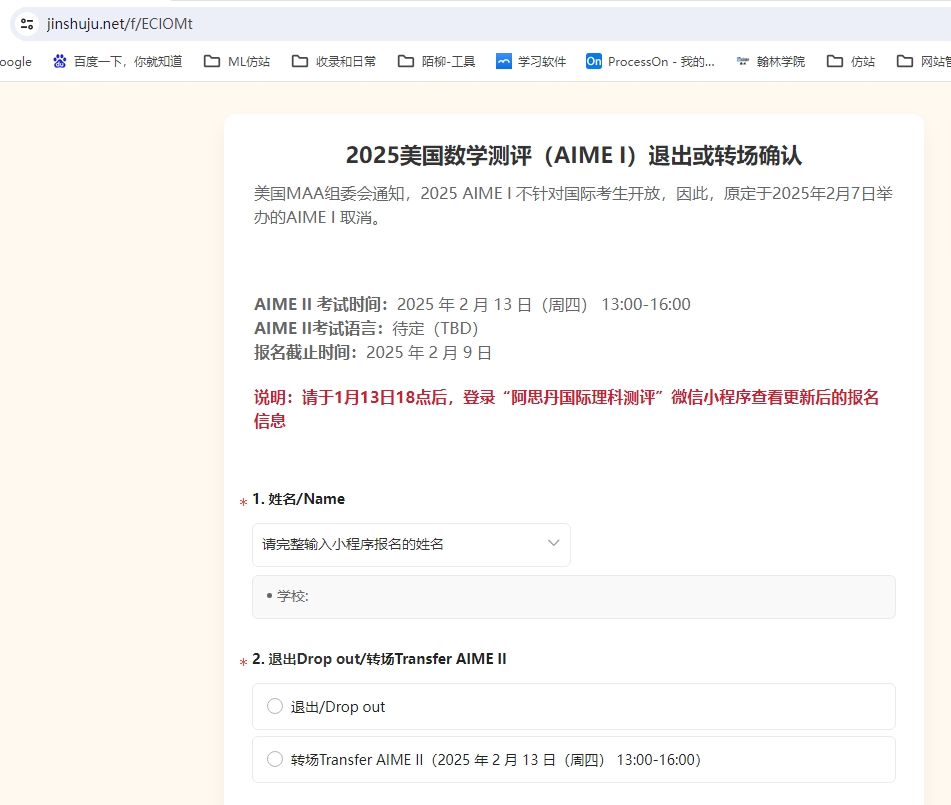
①2025年AIMEI不针对国际考生开放,因此原定于国内2025年2月7日举办的AIME I 取消,已报名的学生请于1月13日(周一)10:00前点击链接登记:https://jinshuju.net/f/EClOMt,确认退出或转场至2月13日举办的AIME II 。如有疑问,请联系:400-9999-615(9:00-18:00)
②AIME II (2025年2月13日周四13:00-16:00)考试语言确定为中英文。
二、AIME考试内容
代数知识
多项式:掌握多项式的运算及因式分解技巧,如综合除法和待定系数法。
函数:理解一次函数、二次函数、三角函数等的性质,如单调性和周期性。
方程与不等式:熟悉一元一次方程、一元二次方程及不等式的解法,应用均值不等式等技巧。
几何知识
平面几何:熟练掌握三角形、四边形、圆等图形的性质和定理,如相似定理、圆周角定理。
立体几何:掌握棱柱、棱锥等几何体的表面积和体积公式,应用空间向量解决立体几何问题。
数论基础
整除理论:理解整除、余数、最大公因数等概念,应用辗转相除法求最大公因数。
同余问题:掌握同余的基本性质和定理,求解同余方程。
重点问题
排列组合:掌握排列数、组合数的计算及应用,解决复杂的排列组合问题。
概率基础:了解古典概型和几何概型,计算简单事件的概率。
四、AIME竞赛考试形式和备考建议
考试形式与评分
形式:线上比赛,中英双语
题目:共15道填空题,每题1分,满分15分
时长:3小时
备赛建议
题目难度与时间分配
第1-6题:难度与AMC10/12相当,建议120分以上的同学不花太多时间,控制在30-40分钟。
第7-10题:过渡题,需对排列组合、二项式定理、韦达定理等知识点有高熟练度,建议花费30-40分钟。
第11-15题:难度较大,建议从擅长的题目开始,确保基础题答对,最终拿奖是关键。
做题策略
避免穷举:不要大量分类,做一道就检查一道。
使用A4草稿纸:对折后清楚写下计算步骤,方便检查。
二次检查:用代入法、特殊值法等进行二次检查,确保准确。
知识点掌握
高频考点:排列组合与数论、不定方程、韦达定理等。
计算能力:提高手动计算的准确性和速度。
AIME作为美国数学竞赛体系中的重要环节,不仅是通往USAMO的必经之路,也是展示学生数学能力的绝佳机会。通过积极备考和充分准备,学生不仅能在AIME中取得优异成绩,还能为未来的学术和职业发展打下坚实基础。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓




2025 AIME竞赛最新变动!!!
根据美国数学协会(Mathematics Association of America, MAA)组委会最新发布的通知,2025年的美国数学邀请赛(AIME I)将不再面向海外开放,这意味着中国地区的AIME I赛事也将被取消。然而,AIME II仍正常举办,时间定于2025年2月13日,关于试卷语言的具体安排尚未公布。

AIME赛事概述及规则
AIME,即美国数学邀请赛(American Invitational Mathematics Examination),是美国数学竞赛体系中的重要环节,为在数学领域表现优异的学生提供了进一步展示能力的平台。赛事的目标不仅在于发掘和培养数学天赋,还为美国国家队选拔国际数学奥林匹克(IMO)参赛选手奠定基础。
AIME通常分为两场考试:AIME I和AIME II,时间相隔约一周。每位学生只能选择参加其中一场,任何试图同时参加两场考试的行为都将被取消资格。2025年,AIME II的考试时间为2月13日。对于已经通过ASDAN报名参加AIME I的学生,需在2025年1月13日10点前通过指定链接完成登记,确认退出或转至AIME II。登记链接为:https://jinshuju.net/f/ECIOMt。
赛事规则方面,AIME考试包括15道简答题,考试时长为3小时。试题语言通常为英语,要求考生具备扎实的数学基础和一定的英语阅读及理解能力。考试内容涵盖代数、几何、数论和组合数学四大领域,其难度较AMC10和AMC12更高,旨在考查学生灵活运用数学知识解决复杂问题的能力。
具体来说:
AIME的晋级与影响
只有在美国数学竞赛10(AMC10)或美国数学竞赛12(AMC12)中达到一定成绩标准的学生,才有资格参加AIME。通常,AMC10排名前2.5%的学生和AMC12排名前5%的学生可获得晋级资格。具体分数线会根据每年的考试整体情况进行调整。AIME的满分为15分,得分在7至10分之间的考生在申请美国顶尖大学时将占据明显优势,而得分超过10分的考生则有机会进入美国数学奥林匹克(USAMO)。
AIME成绩不仅是美国大学录取参考的重要指标,也是培养数学精英的重要一环。通过AMC10、AMC12及AIME的层层筛选,优秀学生将晋级USAMO(美国数学奥林匹克),其地位相当于中国的全国高中数学联赛(CMO)。USAMO优胜者将进一步进入数学奥林匹克夏令营(MOSP),最终选拔出6名顶尖选手代表美国参加国际数学奥林匹克(IMO)。
需要注意的是,IMO仅对具有美国国籍的学生开放,这意味着国际学生无法通过该体系参与IMO的最终比赛。
美国数学竞赛(AMC)简介
美国数学竞赛(American Mathematics Competition, AMC)由美国数学协会于1950年创立,是全球范围内最具可信度和挑战性的数学竞赛之一。其试题设计从简单到复杂,适合不同数学水平的学生参与,同时也能够激励学生突破自身极限。
AMC的系列赛事包括AMC8、AMC10和AMC12:
AMC成绩在美国大学申请中具有重要作用,尤其是对申请麻省理工学院(MIT)、斯坦福大学、卡内基梅隆大学等顶尖学府的学生而言。此外,AMC成绩也被中国许多重点高校所认可。对于中国学生来说,由于普遍具备较强的数学基础,AMC及其相关赛事成为展示个人学术能力的良好机会。
赛事的意义与价值
参加AMC及AIME不仅是数学爱好者展示才华的平台,更是进入顶尖高校的敲门砖。美国数学协会组织的竞赛体系以其严谨性和科学性闻名,试题由哈佛大学、普林斯顿大学等顶尖学府的教授设计和评审,确保了比赛的高水准。此外,AMC还得到了美国中学校长协会的高度推荐,被列为每年学校的重要活动之一。
对于中国学生而言,参与AMC和AIME不仅能够提升数学能力,还能在国际舞台上展示自己的学术实力。随着2025年AIME I对海外关闭,中国考生需要更多关注AIME II的安排,同时利用AMC和AIME提供的机会,为未来的学术和职业发展打下坚实基础。
总之,AIME作为全球数学竞赛的重要组成部分,其影响力不仅局限于数学领域,更为学生的综合能力发展提供了广阔的舞台。在全球化的背景下,参与这样的赛事将为学生的未来创造更多可能性。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓



AIME(American Invitational Mathematics Examination)是美国数学邀请赛,是AMC10和AMC12的晋级赛事,专为在这些竞赛中表现优异的学生而设。AIME不仅是进入美国数学奥林匹克(USAMO)的必经阶段,也是展示学生数学能力的绝佳平台。随着2025年AIME竞赛临近,本文将详细介绍AIME的考试安排、知识体系、参赛资格及报名流程,帮助学生为这一重要赛事做好准备。
一、2025年AIME竞赛安排
考试时间与地点
AIME I:2025年2月7日 13:00-16:00(美国时间)
AIME II:2025年2月13日 13:00-16:00(美国时间)
考试形式为在线考试,语言为中英双语。
试卷构成
15道填空题,答案为000-999之间的整数。
每题1分,满分15分。
重要提醒
晋级AIME的学生无需重新报名,但需进行报名确认。学生可选择参加AIME I或AIME II,但不能同时参加。
二、AIME考试内容
代数知识
多项式:掌握多项式的运算及因式分解技巧,如综合除法和待定系数法。
函数:理解一次函数、二次函数、三角函数等的性质,如单调性和周期性。
方程与不等式:熟悉一元一次方程、一元二次方程及不等式的解法,应用均值不等式等技巧。
几何知识
平面几何:熟练掌握三角形、四边形、圆等图形的性质和定理,如相似定理、圆周角定理。
立体几何:掌握棱柱、棱锥等几何体的表面积和体积公式,应用空间向量解决立体几何问题。
数论基础
整除理论:理解整除、余数、最大公因数等概念,应用辗转相除法求最大公因数。
同余问题:掌握同余的基本性质和定理,求解同余方程。
重点问题
排列组合:掌握排列数、组合数的计算及应用,解决复杂的排列组合问题。
概率基础:了解古典概型和几何概型,计算简单事件的概率。
三、AIME参赛资格和报名情况
参赛资格
AIME I和II的参赛资格与AMC成绩相关。在AMC10/12中达到一定分数线的学生有资格参加AIME。某些地区或学校可能会根据实际情况灵活安排参赛资格。
报名灵活性
学生通常通过学校统一报名AIME I。如果错过机会或报名人数已满,可以通过其他渠道报名AIME II,如直接向竞赛官方机构咨询个人报名方式。
四、AIME竞赛备考建议
系统复习:全面梳理代数、几何、数论等知识点,针对薄弱环节进行强化训练。
模拟练习:通过历年真题进行模拟考试,熟悉题型和考试节奏。
策略调整:根据模拟考试结果调整学习策略,确保在考试中发挥最佳水平。
AIME作为美国数学竞赛体系中的重要环节,不仅是通往USAMO的必经之路,也是展示学生数学能力的绝佳机会。通过积极备考和充分准备,学生不仅能在AIME中取得优异成绩,还能为未来的学术和职业发展打下坚实基础。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓




美国数学邀请赛(AIME)是国际数学竞赛中极具影响力的赛事之一,难度高于AMC10和AMC12。AIME的成绩在大学申请中扮演着重要角色,优秀的成绩不仅为学生增添光彩,还可能晋级至美国数学奥林匹克竞赛(USAMO)。本文将详细介绍AIME的考试须知、题目内容与难度,以及其成绩的用途和认可度。
一、AIME考试须知
考试形式与评分
形式:线上比赛,中英双语
题目:共15道填空题,每题1分,满分15分
时长:3小时
考试安排
AIME I:2025年2月6日
AIME II:2025年2月12日
学生可以选择参加AIME I或AIME II,但不能同时参加,否则将取消资格。
晋级与成绩
获得7-10分对大学申请有很大优势,10分以上通常可晋级USAMO。
二、AIME与AMC的区别分析
题型与难度
AIME:填空题,要求解题并填上答案,难度显著高于AMC。
AMC:选择题,可通过多种方法选择答案。
图形与计算复杂度
AIME:几何题目复杂度高,计算量大,要求多知识点的串联。
AMC:考察基本定义,计算相对简单。
知识点串联与做题速度
AIME:后几题常串联多个知识点,要求快速且准确。
AMC:允许通过猜测或技巧解题。
三、AIME题目内容和难度
整体难度
AIME I和II卷难度相当,均为15道填空题,考查数学综合运用能力和解题技巧。
题目差异
虽难度相同,但I卷和II卷题目不同,知识点组合和表述风格可能有所差异。
涉及领域
代数、几何、数论、组合等多个方面。
四、AIME成绩用途和认可度
成绩用途
AIME成绩在数学竞赛选拔(如USAMO)中具有相同的价值,是评估学生数学能力的重要依据。
认可度
在大学申请中,AIME成绩被广泛认可,能够证明学生在数学方面的高能力。
题目风格偏好
考生可以根据自身对某种题目风格的偏好选择参加I卷或II卷,但这种差异通常很小。
AIME竞赛不仅是对学生数学能力的考验,也是提升他们学术背景的重要机会。通过合理的备考策略,学生可以在AIME中脱颖而出,获得更多参与高级别竞赛的机会,为未来的学术和职业发展奠定坚实基础。AIME是数学爱好者展示才华的理想平台。
备赛的同学可免费下载
AIME竞赛真题集+答案+300道精讲题+分类题册+梯度题册+解析等干货⇓



