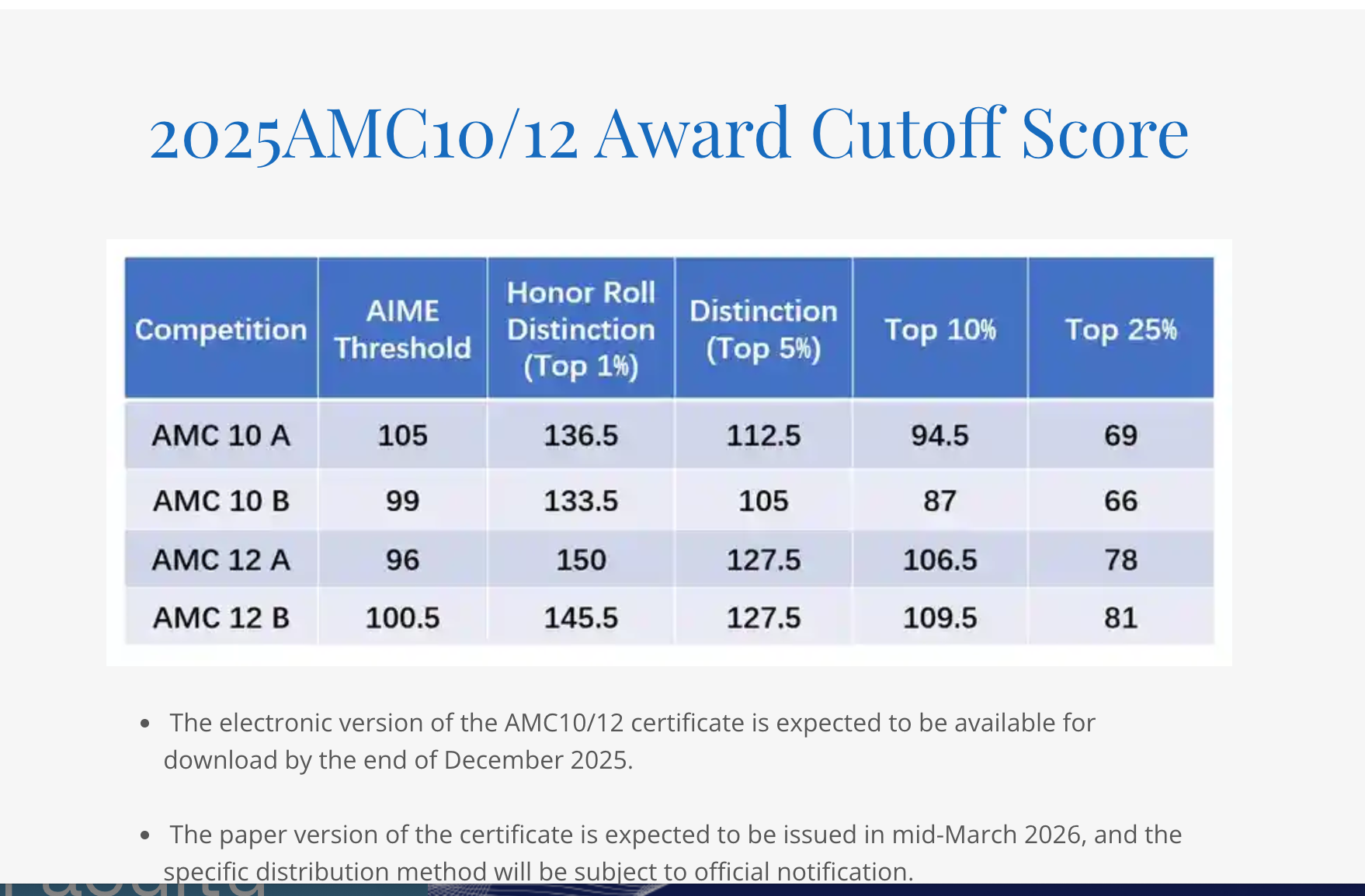
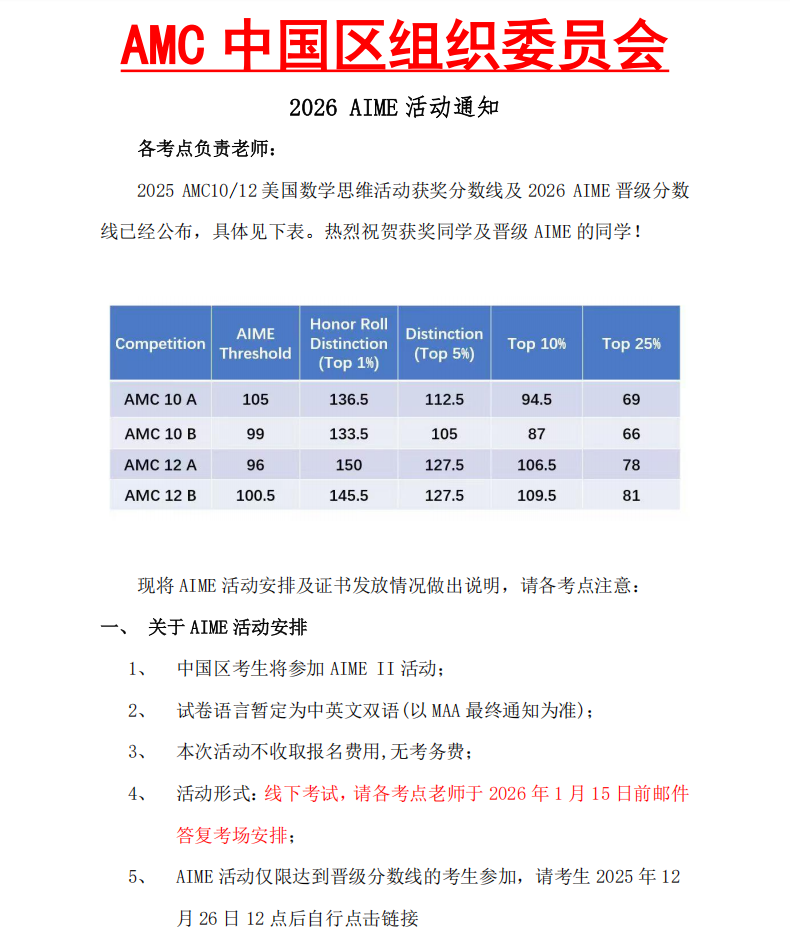
2026年AIME数学竞赛的脚步声越来越近。对已获得参赛资格的学子而言,这最后阶段的冲刺质量,将直接决定最终成绩。随着2026年AIME权重在USA(J)MO晋级公式中从10倍提升至20倍,每一分的价值都变得前所未有的重要。
这场考试不仅考察数学知识,更考验时间管理、应变能力和心理素质。在有限的备考时间内,精准发力比盲目努力更重要。
一、2026年AIME赛程安排
考试时间与基本安排
2026年AIME竞赛分为两场进行,具体时间安排如下:
AIME I卷:2026年2月6日(周四)13:00-16:00
AIME II卷:2026年2月12日(周三)13:00-16:00
报名截止日期:2026年1月27日
2026年AIME竞赛基本信息概览
|
项目
|
具体内容
|
|---|---|
|
参赛资格
|
AMC10前2.5%左右或AMC12前5%左右
|
|
考试时长
|
3小时
|
|
题型题量
|
15道填空题
|
|
答案格式
|
000-999之间的整数
|
|
评分标准
|
每题1分,答错不扣分,满分15分
|
|
考试语言
|
中英双语
|
|
计算器政策
|
不允许使用
|
规则重大变化
2026年AIME竞赛规则迎来重大调整:AIME分数在USAMO/USAJMO晋级中的权重从10倍提升至20倍。
全新的晋级公式为:
USAMO指数 = AMC12分数 + 20 × AIME分数
USAJMO指数 = AMC10分数 + 20 × AIME分数
这一变化使AIME分数在总分中的占比从约50%跃升至约2/3,显著提升了AIME成绩的重要性。
二、题目难度分布与时间分配策略
AIME竞赛的题目难度呈明显的梯度递增特征。理解这一规律并据此制定时间分配策略,是取得理想成绩的关键。
AIME题目难度分布与应考策略
|
题号范围
|
难度描述
|
推荐用时
|
目标分数策略
|
|---|---|---|---|
|
1-5题
|
中等难度,相当于AMC12的15-18题
|
30-40分钟
|
必须确保全对,基础得分点
|
|
6-10题
|
难度显著提升,多知识点综合
|
50分钟左右
|
冲7+分的关键,力争高分
|
|
11-15题
|
高难度题目,接近USAMO水平
|
至少30-40分钟
|
区分顶尖学生的关键
|
时间管理是AIME考试中的核心挑战。平均每道题只有12分钟解题时间,但实际分配应遵循“前紧后松”的原则。前5题应控制在40分钟内完成,这些题目相对简单,是基础得分点,不宜匆忙作答导致失误。
中间5题(6-10题)是获得竞争优势的关键,建议用50分钟左右时间,这些题目通常需要综合运用多个知识点。最后5题至少保留30分钟时间,即使无法完全解出,也应尝试获取部分分数。
三、四大模块重难点深度解析
1、代数模块
代数在AIME中占比最高,达到35%-40%。高频考点包括高次方程、韦达定理、复数、不等式、数列和函数方程。
备考重点:
复数与三角函数结合的问题,特别是单位根的应用
递归数列的通项求解与周期性分析
复杂不等式的证明技巧,尤其是柯西不等式和均值不等式的灵活运用
易错点提醒:代数变形中的符号错误是常见失分点,多步骤问题需进行端点值验证,防止漏解。
2、几何模块
几何在AIME中占比30%-35%,包括平面几何、解析几何和立体几何。
核心难点:
三角形多心问题(外心、内心、重心、垂心)及其性质综合应用
圆幂定理、根轴与根心、位似变换等高级定理的理解与运用
解析几何与三角函数、复数方法的结合应用
策略建议:AIME的几何题目较少直接使用特殊定理(如梅涅劳斯、塞瓦),而是更注重基础性质的综合运用和三角方法的熟练度。三角函数在解决几何问题中尤为重要,特别是中高编号的题目,找到关键角并应用正、余弦定理建立边角关系是解题核心。
3、数论模块
数论占比约15%-20%,是AIME后5题的主要难点所在。
必须掌握的高阶知识点:
同余理论与中国剩余定理的应用场景
高次同余方程,特别是费马小定理与欧拉定理的应用
LTE引理在整除性问题中的应用
备考建议:数论题目逻辑链条长,需要严密的推理能力和构造性思维。通过模运算缩小解的范围,或利用数的表示形式(如p进制)解决问题是常见思路。
4、组合数学
组合数学占比约10%-15%,是另一大难点板块。
重点难点:
递推关系与递归思想的应用
生成函数计数与组合恒等式
复杂概率计算与几何概型
应对策略:组合题目常需构建数学模型,将实际问题转化为“球与盒子”或“路径计数”等经典模型。培养“组合直觉”和模型构建能力至关重要。
四、三阶段冲刺备考计划
阶段一:诊断补漏(现在至1月底)
限时3小时完成一套近三年真题,模拟真实考试环境
按四大模块统计正确率,精准定位薄弱环节
针对性复习薄弱知识点的高频考点和解题方法
阶段二:专项攻坚(1月底至2月初)
针对弱势模块开展专题训练
精做2015-2020年真题中的相关题目,重点练1-10题
建立错题本,系统归纳错误类型(知识漏洞/计算失误/思路偏差)
阶段三:模考冲刺(2月初至考前)
每2-3天完成一套全真模考,严格模拟3小时考试环境
优化时间分配策略,找到最适合自己的答题节奏
重点训练对难题的“破题”感觉,形成自己的解题节奏
五、考场实战技巧与易错点提醒
核心解题技巧
数字规律探索:将复杂问题简化为小规模案例,观察序列规律。
特殊值代入:对于函数方程、对称性问题,尝试代入0、1、-1等简单值。
图形辅助:几何题务必画精准图,组合题用树状图、表格梳理状态。
对称性原理:若结构对称,答案常为整数或特殊值,可据此验证结果合理性。
常见易错点及避免方法
|
易错点类型
|
具体表现
|
避免方法
|
|---|---|---|
|
答案格式错误
|
未写成三位数(如答案“5”写成“5”而非“005”)
|
交卷前专项检查所有答案格式
|
|
计算粗心
|
符号错误、余数算错、步骤遗漏
|
关键步骤反复验算,利用对称性验证
|
|
时间分配不当
|
在前几题耗费过多时间,导致后题匆忙
|
严格遵循时间分配计划,果断跳过难题
|
|
思路僵化
|
固执于一种解法,不尝试替代思路
|
每道题限时思考3-5分钟,无进展则标记后跳过
|
心态调整建议
AIME竞赛的题目难度确实较高,即使对于经验丰富的考生,完成所有题目也是一大挑战。遇到难题时保持冷静,记住即使顶尖学生也未必能全部解出。确保已掌握题目的高准确率,部分解出难题也能获得部分分数。
距离2026年AIME竞赛开赛还有不到一个月的时间,每一天都弥足珍贵。制定科学的备考计划,保持稳定的学习节奏,避免临考前过度劳累影响状态。最终的成功不仅取决于知识储备,更取决于临场心态和策略选择。
扫码进入AIME专属学习社群,海量备赛资料&体验课程等你开启!
备赛的同学可扫码免费下载
1983-2025年AIME真题&解析+分类题库/梯度题库&解析+考前必练300题+解析+备赛书单⇓