2016年 AIME II 数学邀请赛真题

2016年 AIME II 数学邀请赛真题

问题 1

最初，亚历克斯、贝蒂和查理共有 $444$ 花生。查理的花生最多，亚历克斯的花生最少。每个人拥有的三个花生数量形成一个等比级数。亚历克斯吃掉 $5$ 他的花生，贝蒂吃掉 $9$ 她的花生，查理吃掉 $25$ 他的花生。现在每个人拥有的三个花生数量形成了一个等差级数。求出亚历克斯最初拥有的花生数量。

问题 2

$40\%$ 周六有下雨的概率， $30\%$ 周日也有下雨的概率。但是，如果周六下雨，周日下雨的概率是周六不下雨的两倍。本周末至少有一天下雨的概率是 $\frac{a}{b}$ ，其中 $a$ 和 $b$ 是互质正整数。求 $a+b$ 。

问题 3

设 $x,y,$ 和 $z$ 为满足系统实数 $\begin{align*} \log_2(xyz-3+\log_5 x)&=5,\\ \log_3(xyz-3+\log_5 y)&=4,\\ \log_4(xyz-3+\log_5 z)&=4。\end{align*}$ 求出的值 $|\log_5 x|+|\log_5 y|+|\log_5 z|$ 。

问题4

一个 $a \乘以 b \乘以 c$ 矩形盒子由单位立方体构成 $a \cdot b \cdot c$ 。每个单位立方体的颜色为红色、绿色或黄色。与盒子表面平行 $a$ 的每层大小恰好包含红色立方体、绿色立方体和一些黄色立方体。与盒子表面平行的每层大小恰好包含绿色立方体、黄色立方体和一些红色立方体。求出盒子的最小可能体积。 $1 \乘以 b \乘以 c$ $(b\乘以c)$ $9$ $12$ $b$ $a \times 1 \times c$ $(a \times c)$ $20$ $25$

问题5

三角形 $ABC_0$ 在处有一个直角 $C_0$ 。其边长是两两互质的正整数，其周长为 $p$ 。设 $C_1$ 为的高脚到 $\overline{AB}$ ，对于 $n \geq 2$ ，设为中 $C_n$ 的高脚到。和。求。 $\overline{C_{n-2}B}$ $\三角形 C_{n-2}C_{n-1}B$ $\sum_{n=2}^\infty C_{n-2}C_{n-1} = 6p$ $p$

问题 6

对于多项式 $P(x)=1-\dfrac{1}{3}x+\dfrac{1}{6}x^{2}$ ，定义 $Q(x)=P(x)P(x^{3})P(x^{5})P(x^{7})P(x^{9})=\sum_{i=0}^{50} a_ix^{i}$ 。然后 $\sum_{i=0}^{50} |a_i|=\dfrac{m}{n}$ ，其中 $百万$ 和 $n$ 是互质正整数。求 $m+n$ 。

问题 7

正方形 $ABCD$ 和 $EFGH$ 有共同的中心和 $\overline{AB} || \overline{EF}$ 。的面积 $ABCD$ 是2016，的面积 $EFGH$ 是较小的正整数。正方形 $IJKL$ 的构造使得它的每个顶点都位于的边上 $ABCD$ ，而的每个顶点都 $EFGH$ 位于的边上 $IJKL$ 。求出面积的最大值和最小值之间的差值 $IJKL$ 。

问题 8

$\{a,b,c\}$ 求出具有以下性质的三个不同正整数集的数量： $a,b,$ 和的乘积 $c$ 等于 $11,21,31,41,51,$ 和的乘积 $61$ 。

问题 9

正整数序列 $1，a_2，a_3，...$ 和 $1,b_2,b_3,...$ 分别是递增的等差序列和递增的等比序列。设 $c_n=a_n+b_n$ 。存在一个整数 $k$ 使得 $c_{k-1}=100$ 和 $c_{k+1}=1000$ 。求 $c_k$ 。

问题 10

三角形 $ABC$ 内接于圆 $\omega$ 。点 $P$ 和 $Q$ 位于边 $\overline{AB}$ 。 $AP<AQ$ 射线 $CP$$ 和分别在和处再次 $CQ$ 相交（除外）。若和，则，其中和为互质正整数。求。 $\omega$ $S$ $T$ $加元$ $AP=4,PQ=3,QB=6,BT=5,$ $AS=7$ $ST=\frac{m}{n}$ $百万$ $n$ $m+n$

问题11

对于正整数 $N$ 和 $k$ ，如果存在一个正整数，并且恰好有正因数，则定义 $N$ 为-nice 。找出小于的正整数的数量，既不是-nice的也不是-nice的。 $k$ $a$ $a^{k}$ $N$ $1000$ $7$ $8$

问题 12

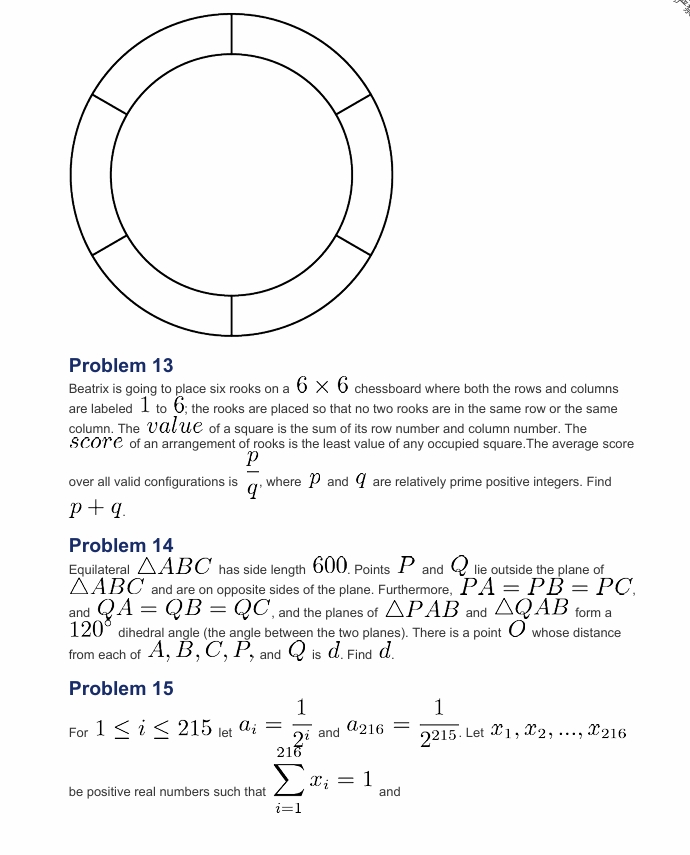
下图显示了一个由六个小部分组成的环，您要将其涂在墙上。您有四种油漆颜色可供选择，您将为六个部分涂上纯色。如果相邻的两个部分不能涂上相同的颜色，请找出您可以选择的涂漆方式的数量。

$[asy] 绘制（圆（（0,0），4））；绘制（圆（（0,0），3））；绘制（（0,4）--（0,3））；绘制（（0，-4）--（0，-3））；绘制（（-2.598，1.5）--（-3.4641，2））；绘制（（-2.598，-1.5）--（-3.4641，-2））；绘制（（2.598，-1.5）--（3.4641，-2））；绘制（（2.598，1.5）--（3.4641，2））；[/asy]$

以下是我们为您整理的全英版pdf真题：

扫码免费获取完整版真题+解析~~~

我们整理了近十年全部AMC备赛资料，包括AMC8/10/12/AIME的历年真题和答案详解，备赛书籍、知识点地图、备赛公式等，