2012年 AIME I 数学邀请赛真题
问题 1
求出具有三个不一定不同的数字的正整数的数量,![]() 其中和
其中和![]() ,并且和
,并且和![]() 都是的倍数。
都是的倍数。 ![]()
![]()
![]()
问题 2
等差数列的项加起来为![]() 。数列的第一项增加
。数列的第一项增加![]() ,第二项增加
,第二项增加![]() ,第三项增加
,第三项增加![]() ,一般来说,
,一般来说,![]() 第 项增加
第 项增加![]() 第 奇数个正整数。新数列的项加起来为
第 奇数个正整数。新数列的项加起来为![]() 。求原数列第一项、最后一项和中间项的和。
。求原数列第一项、最后一项和中间项的和。
问题 3
九个人坐下来吃饭,有三种餐点可供选择。三个人点了牛肉餐,三个人点了鸡肉餐,三个人点了鱼肉餐。服务员以随机顺序提供九种餐点。求出服务员为九个人提供餐点的方式数量,使得只有一个人收到他点的餐点。
问题4
布奇和桑德斯需要离开道奇。为了尽快出发,他们轮流步行和骑着他们唯一的马斯帕基,如下所示。布奇先步行,桑德斯骑马。当桑德斯到达沿途每隔一英里就有一个拴马桩时,他把斯帕基拴在桩上,然后开始步行。布奇到达斯帕基时,他骑马直到经过桑德斯,然后在下一个拴马桩留下斯帕基,继续步行,就这样继续下去。斯帕基、布奇和桑德斯的步行速度分别为![]()
![]() 和
和![]() 英里每小时。布奇和桑德斯第一次在里程碑处相遇时,他们
英里每小时。布奇和桑德斯第一次在里程碑处相遇时,他们![]() 距离道奇有数英里,并且已经旅行了
距离道奇有数英里,并且已经旅行了![]() 几分钟。求
几分钟。求![]() 。
。
问题5
设是所有可以用零和一(允许前导零)![]() 书写的二进制整数的集合。如果执行所有可能的减法,其中一个元素从另一个元素中减去,求出得到 答案的次数。
书写的二进制整数的集合。如果执行所有可能的减法,其中一个元素从另一个元素中减去,求出得到 答案的次数。![]()
![]()
![]()
![]()
问题 6
复数![]() 和
和![]() 满足
满足![]()
![]() ,且的虚部为
,且的虚部为![]() ,
,![]() 对于互质正整数
对于互质正整数![]() ,
,![]() 且
且![]() 查找
查找![]()
问题 7
下图网络中的 16 个圆圈中,每个圆圈旁边都站着一名学生。16![]() 名学生共分配了 100 枚硬币。所有学生同时将相同数量的硬币传递给网络中的每位邻居,从而将所有硬币赠送出去。交易后,所有学生的硬币数量与开始时相同。求出站在中心圆圈的学生最初拥有的硬币数量。
名学生共分配了 100 枚硬币。所有学生同时将相同数量的硬币传递给网络中的每位邻居,从而将所有硬币赠送出去。交易后,所有学生的硬币数量与开始时相同。求出站在中心圆圈的学生最初拥有的硬币数量。
![[asy] 导入cse5;单位尺寸(6mm);默认笔(线宽(.8pt));点因子 = 8;路径笔=黑色;对 A = (0,0);对 B = 2*dir(54),C = 2*dir(126),D = 2*dir(198),E = 2*dir(270),F = 2*dir(342);对 G = 3.6*dir(18),H = 3.6*dir(90),I = 3.6*dir(162),J = 3.6*dir(234),K = 3.6*dir(306);对 M = 6.4*dir(54),N = 6.4*dir(126),O = 6.4*dir(198),P = 6.4*dir(270),L = 6.4*dir(342);对[]点状 = {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P};D(A--B--H-- M); D(A--C--H--N); D(A--F--G--L); D(A--E--K--P); D(A-- D--J--O); D(B--G--M); D(F--K--L); D(E--J--P); D(O--I-- D); D(C--I--N); D(L--M--N--O--P--L); 点(虚线);[/asy]](https://latex.artofproblemsolving.com/3/3/a/33abde80848746d240bfc392b8997b80cf3bccd5.png)
问题 8
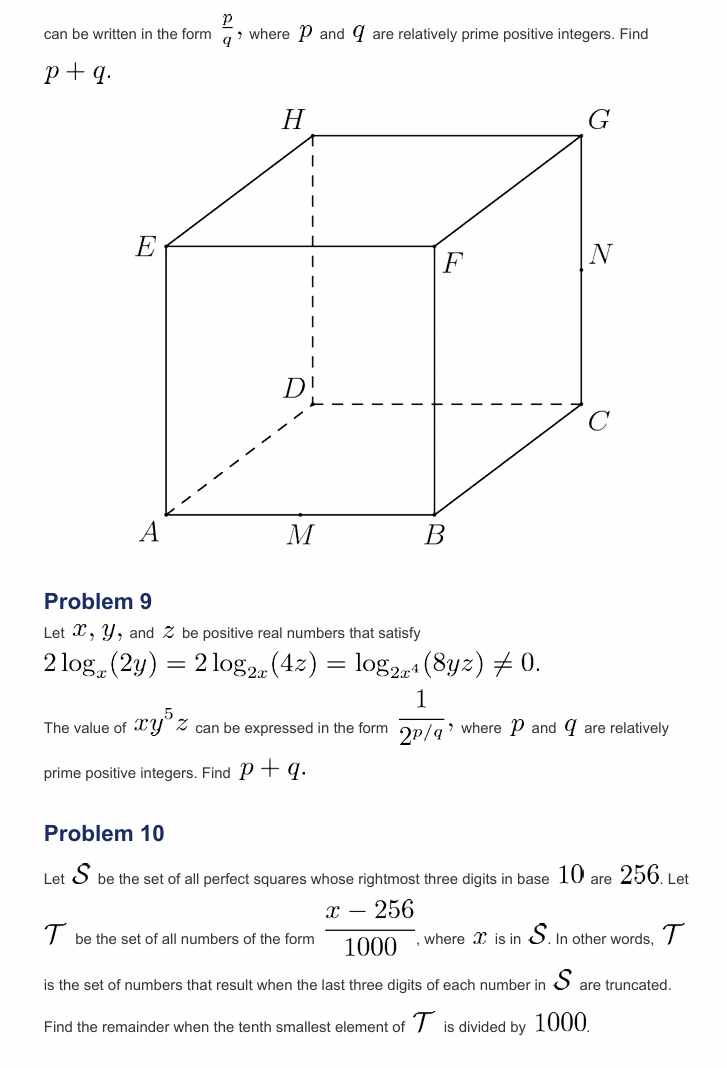
![]() 如下所示的立方体,其边长为,被一个通过顶点和中点和的
如下所示的立方体,其边长为,被一个通过顶点和中点和的![]() 平面切割。该平面将立方体分成两个立体。两个立体中较大立体的体积可以写成如下形式,其中和是互质正整数。求
平面切割。该平面将立方体分成两个立体。两个立体中较大立体的体积可以写成如下形式,其中和是互质正整数。求![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[asy]import cse5; unitize(10mm); pathpen=black; dotfactor=3; pair A = (0,0), B = (3.8,0), C = (5.876,1.564), D = (2.076,1.564), E = (0,3.8), F = (3.8,3.8), G = (5.876,5.364), H = (2.076,5.364), M = (1.9,0), N = (5.876,3.465); pair[] dotted = {A,B,C,D,E,F,G,H,M,N}; D(A--B--C--G--H--E--A); D(E--F--B); D(F--G); pathpen=dashed; D(A--D--H); D(D--C); dot(dotted);标签(“$A$”,A,SW);标签(“$B$”,B,S);标签(“$C$”,C,SE);标签(“$D$”,D,NW);标签(“$E$”,E,W);标签(“$F$”,F,SE);标签(“$G$”,G,NE);标签(“$H$”,H,NW);标签(“$M$”,M,S);标签(“$N$”,N,NE); [/asy]](https://latex.artofproblemsolving.com/a/f/1/af154db9d25256bd90239e9f4e37253b234659e0.png)
问题 9
设![]()
![]() 和
和![]() 为满足的正实数,
为满足的正实数,![]() 的值
的值![]() 可以表示为其中
可以表示为其中![]() 和
和![]() 为
为![]() 互质正整数。求
互质正整数。求![]()
问题 10
设![]() 为底数最右边三位为 的所有完全平方数的集合
为底数最右边三位为 的所有完全平方数的集合![]() 。
。![]() 设
设![]() 为所有形式为 的数的集合
为所有形式为 的数的集合![]() ,其中
,其中![]() 为 中的
为 中的![]() 。换句话说,
。换句话说,![]() 是截断 中每个数的后三位后所得的数的集合
是截断 中每个数的后三位后所得的数的集合![]() 。求 的第十小元素
。求 的第十小元素![]() 除以后的余数
除以后的余数![]() 。
。
问题11
一只青蛙从 开始![]() ,按照以下规则进行一系列跳跃:从 开始,
,按照以下规则进行一系列跳跃:从 开始,![]() 青蛙跳到 ,
青蛙跳到 ,![]() 可以是 中的任何点
可以是 中的任何点![]()
![]()
![]() 或
或![]() 有
有![]() 点可以通过一系列这样的跳跃到达。当 除以 时,求
点可以通过一系列这样的跳跃到达。当 除以 时,求![]() 余数
余数![]()
![]()
![]()
问题 12
设![]() 是直角三角形,直角位于 设
是直角三角形,直角位于 设![]() 和
和![]() 是
是![]() 上的点,
上的点,![]() 位于和
位于和![]() 之间,使得和三等分如果则可写成 其中和是互质正整数,并且是不能被任何素数的平方整除的正整数。求
之间,使得和三等分如果则可写成 其中和是互质正整数,并且是不能被任何素数的平方整除的正整数。求![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
以下是我们为您整理的全英版pdf真题:
扫码免费获取完整版真题+解析~~~
还可免费下载1983-2025年AIME I&II中英文真题+解析+各类题库&解析+书单等⇓



